• Regression Model - {:.} Error Term
• Least Squares Estimation - {:.} Data - {:.} Numpy로 구현 - {:.} Numpy with Matrix 구현 - {:.} Numpy with Linalg 구현 - {:.} Statsmodels OLS
• Multiple Regression with Matrix (Least Squares Estimation) - {:.} Sum of the Squared Estimation with Matrix - {:.} Derivative of SSE - {:.} Data - {:.} Numpy 구현 - {:.} Numpy with Linalg 구현 - {:.} Statsmodels 구현

Vladimir Kudinov의 사진
기본으로 돌아가서.. 천천히..

Regression Model

예를 들어 학생별 공부한 시간대비 퀴즈 성적표를 데이터로 쓴다면 다음과 같습니다.

• \(\hat{y}\) : 퀴즈 점수
• \(x\) : 공부한 시간
• \(e_i\) : error term
• \(\beta_{const}\) : y-intercept를 나타내며, 학생이 수업에 나오기만 해도 주는 점수라고 보면 됩니다.
• \(\beta_i\) : 각 학생이 공부한 시간에 따른 추가적인 점수

Error Term

Error Term은 random influences를 나타냅니다.
\(\begin{align} e &= y - \hat{y} \\ y &= \hat{y} + e \end{align}\)

error 값은 input값으로 들어가는 값중의 하나이며, 정하는건… 분석가의 능력에 달려있습니다.
만약 넣지 않으면 \(\beta_{const}\) 에서 y-intercept로 반영이 될 것입니다.

Least Squares Estimation

일단 y값은 데이터이기 때문에 어떤 값인지 알고 있지만, parameters \(\beta\) 값들은 모르기 때문에, 알기 위해서는 어떠한 방법으로 estimate해줘야 합니다.
가장 흔하게 쓰이는 방법은 SSE (Sum of the Squared Error)입니다.

Least sqaures estimation을 calculus로 미분하면 다음과 같은 결과가 나옵니다.

그리고..

Derivation하는 방법은 다음의 문서를 참고합니다.

• Simple Linear Regression Least Squares Estimates of β0 and β1
• The Mathematical Derivation of Least Squares

Data

data = np.loadtxt('../../data/linear-regression/ex1data1.txt', delimiter=',')
scaler = StandardScaler()
data = scaler.fit_transform(data)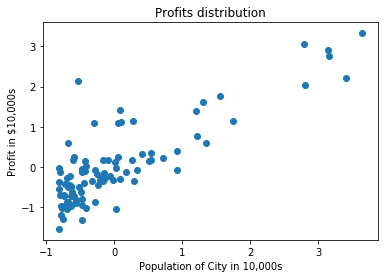

Numpy로 구현

def least_square_estimate(x, y):
    x_mean, y_mean = x.mean(), y.mean()
    w = np.zeros(2)

    w[1] = np.sum((y - y_mean) * (x - x_mean))/ np.sum((x - x_mean)**2)
    w[0] = y_mean - w[1] * x_mean
    return w

def ls_predict(w, x):
    return w[0] + w[1:].dot([x])

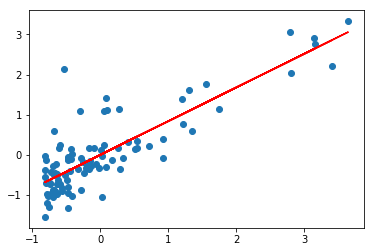
w = least_square_estimate(data[:, 0], data[:, 1])

y_pred = ls_predict(w, data[:, 0])

print('bias:', w[0])
print('beta:', w[1])

scatter(data[:, 0], data[:, 1])
plot(data[:, 0], y_pred, color='red')

bias: 8.46098609281e-16
beta: 0.837873232526

Numpy with Matrix 구현

def least_square_with_matrix(x, y):
    x = sm.add_constant(x)

    a = np.linalg.inv(x.T @ x)
    b = x.T @ y
    B = a @ b
    return B

def predict(B, x):
    x = sm.add_constant(x)
    return x @ B

def visualize(B, x, y_true, y_pred):
    print('bias:', B[0])
    print('beta:', B[1])

    scatter(x, y_true)
    plot(x, y_pred, color='red')

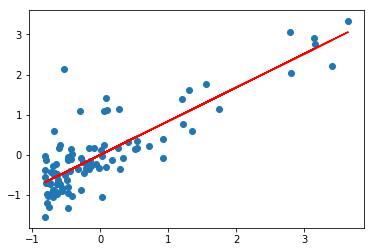
w = least_square_estimate(data[:, 0], data[:, 1])

bias: 8.46098609281e-16
beta: 0.837873232526

Numpy with Linalg 구현

np.linalg.lstsq(
        sm.add_constant(data[:, 0].reshape(-1, 1)),
        data[:, 1].reshape(-1, 1), )[0]
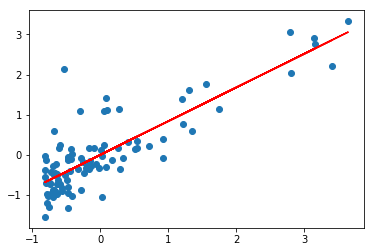
visualize(w, data[:, 0], data[:, 1], y_pred)

bias: 8.46098609281e-16
beta: 0.837873232526

Statsmodels OLS

ols = sm.OLS(data[:, 1], sm.add_constant(data[:, 0]))
ols = ols.fit()
display(ols.summary())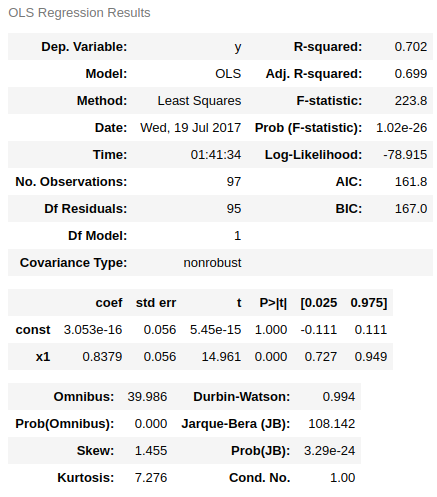

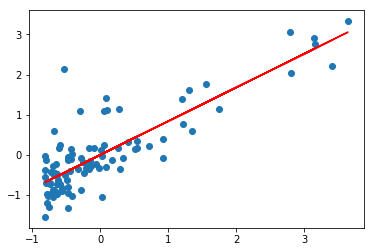
y_pred = ols.predict(sm.add_constant(data[:, 0]))
visualize(ols.params, data[:, 0], data[:, 1], y_pred)

bias: 3.05311331772e-16
beta: 0.837873232526

Multiple Regression with Matrix (Least Squares Estimation)

• The Multiple Regression 중간부분..
• 참고

오직 한개의 independent variable을 갖고서 예측하는 일은 사실.. 매우 드뭅니다.
일반적으로 여러개의 independent variables을 갖고서 한개의 dependent variable을 예측을 하게 됩니다.
Matrix를 사용한 아주 기본적인 (위의 공식) OLS Regression equation 은 다음과 같습니다.

위의 Matrix로 표현될부분을 linear algebra로 다음과 같이 표현될 수 있습니다.

• \(\mathbf{Y}\): N x 1 형태
• \(\mathbf{X}\): N x (k + 1) 형태이며, 첫번째 컬럼은 1로만 구성
• \(\mathbf{B}\): (k + 1) x 1 형태이며, regression constant와 coefficients를 갖고 있음
• \(\mathbf{e}\) : N x 1 형태이며, 예측 에러값을 포함

Sum of the Squared Estimation with Matrix

다음의 loss값을 최소로하는 \(\mathbf{B}\) 를 찾는것이 목표입니다.
SSE는 모든 에러값의 제곱의 합이라고 보면 됩니다. 따라서 \(\mathbf{e}\) 를 제곱한것의 합이기 때문에 다음과 같습니다.

SSE의 중요한 점은 오른쪽 수식을 풀었을때의 답은 scalar값이 나옵니다.
\(\mathbf{B}\) matrix에 관하여 SSE의 미분을 구하고자 한다면 먼저 \(\mathbf{e}\)의 값을 풀어써야 합니다.

여기서 SSE의 오른쪽 공식에 대입하면 다음과 같이 됩니다.

transposition \(\prime\) 은 아래와 같이 distribute될 수 있습니다.

여기서 중간의 2개의 terms \(\mathbf{Y}^{\prime} \mathbf{X} \mathbf{B}\) 그리고 \(\mathbf{B}^{\prime} \mathbf{X}^{\prime} \mathbf{Y}\) 은 동일한 scalar값을 각각 내놓습니다.
scalar값을 내놓은 다는것은 transpose를 해도 동일하다는 뜻입니다. (1 x 1 매트릭스같을수도 있겠죠)
즉.. \(\mathbf{Y}^{\prime} \mathbf{X} \mathbf{B} = \mathbf{B}^{\prime} \mathbf{X}^{\prime} \mathbf{Y}\) 는 transpose를 한쪽에 하면 동일해지기 때문에 이런 공식으로 쓸수 있습니다.

Derivative of SSE

일단 \(\mathbf{B}\)를 제외한 모든 matrix들은 모두 상수로 여깁니다. \(\left( \frac{d}{dx}c = 0 \right)\)
따라서 첫번째 구문 \(\mathbf{Y}^{\prime}\mathbf{Y}\) 그냥 0이 됩니다.

중간부분 \(- 2 \mathbf{Y}^{\prime} \mathbf{X} \mathbf{B}\) 에서 \(\mathbf{B}\)는 없어지고, 나머지 남아있는 matrix에 transpose를 해주면 됩니다.
따라서 \(-2 \mathbf{X}^{\prime} \mathbf{Y}\) 가 됩니다.

그 다음 해줄것은 위에서 구한 식을 0값으로 놓고, \(\mathbf{B}\) 를 구하는 것입니다.

• [1] : 양변을 \(-2 \mathbf{X}^{\prime} \mathbf{X} \mathbf{B}\) 으로 뺌
• [2]: 양변을 -2 로 나눠줌
• [3]: 양변을 \(\mathbf{X}^{\prime} \mathbf{X}\) 의 inverse인 \((\mathbf{X}^{\prime} \mathbf{X})^{-1}\) 로 곱해줍니다. 즉 양변을 \(\mathbf{X}^{\prime} \mathbf{X}\) 으로 나누는 것과 동일합니다.

Data

data = pd.read_csv('../../data/insurance/insurance.csv')
data = pd.get_dummies(data)
display(data.head())

# Split X and Y
data_x = data.loc[:, data.columns!= 'expenses'].as_matrix()
data_y = data['expenses'].as_matrix().reshape((-1, 1))

# Scaling
scaler = StandardScaler()
data_x = scaler.fit_transform(data_x)
data_y = scaler.fit_transform(data_y)

print('train:', data_x.shape)
print('test:', data_y.shape)

Numpy 구현

def least_square_with_matrix(x, y):
    x = sm.add_constant(x)

    a = np.linalg.inv(x.T @ x)
    b = x.T @ y
    B = a @ b
    return B

def predict(B, x):
    x = sm.add_constant(x)
    return x @ B

B = least_square_with_matrix(data_x, data_y)
y_pred = predict(B, data_x)

MSE: 2.21327592281

Numpy with Linalg 구현

B = np.linalg.lstsq(sm.add_constant(data_x), data_y)[0]
y_pred = predict(B, data_x)

MSE: 0.249185764873

Statsmodels 구현

ols = sm.OLS(data_y, sm.add_constant(data_x))
res = ols.fit(method='pinv')
res.summary()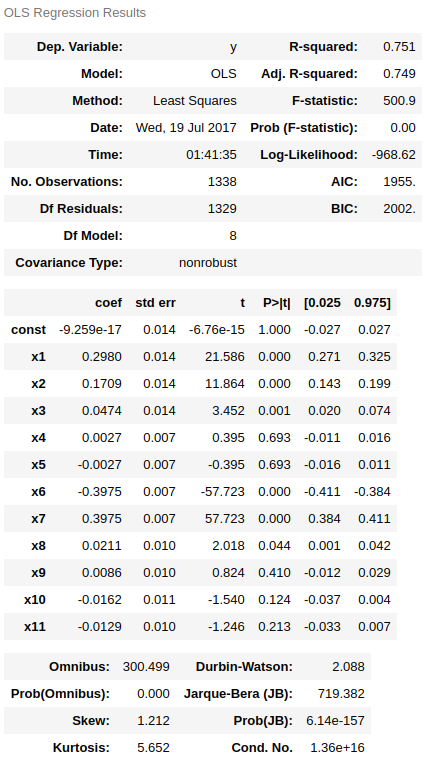

y_pred = res.predict(sm.add_constant(data_x))

MSE: 0.249071533794