ARIMA - Basic Time Series Analysis
- Time Series - {:.} Basic - {:.} Trend, Cyclical, Seasonal, Irregular - {:.} Stationary Time Series
- Data
- Autocorrelation Checking - {:.} Lag Plot - {:.} Pearson Correlation Coefficient - {:.} Autocorrelation Plot
- Lag Operator - {:.} Lag Polynomials - {:.} Invert - {:.} Difference Operator
- AR (Autoregressive) Model - {:.} [Code] Using StatsModels - {:.} [Code] Using Oridinary Least Square Estimation - {:.} [Code] Using Polynomial Curve Fitting
- Moving Average Model
- TODO 작성중입니다.

Time Series
Basic
시간에 따른 일련의 데이터를 Time series data라고 합니다.
단 한개의 변수로 이루어진 time series를 univariate 이라고 하며, 2개 이상의 변수로 이루어진 time series를 multivariate이라고 합니다.
Trend, Cyclical, Seasonal, Irregular
Time series는 일반적으로 4개의 요소 (Trend, Cyclical, Seasonal 그리고 Irregular)에 의해 영향을 받습니다.
| Name | Description |
|---|---|
| Trend(추세) | 장기적인 관점에서 봤을때 그래프가 증가하는지, 감소하는지, 또는 정체되어 있는지등의 추세를 Trend라고 합니다. Trend는 따라서 time series안에서 long term movement를 보는 것이 중요합니다. |
| Seasonality(계절성) | 특정 구간동안의 (1년, 한달, 일주일..) 변동성(fluctuations)를 나타냅니다. 예를 들어서 아이스크림 판매량은 여름에 늘어나고, 외투는 겨운에 판매량이 늘어날 것입니다. 또는 피트니스센터의 고객은 매년 결심을 하는 1월 초에 가장많은 사람들이 나올것입니다. 하지만 매월초가 될수도 있고, 매주초가 될 수도 있습니다. 따라서 피트니스센터는 년, 월, 주단위 seasonality를 갖고 있다고 할수 있습니다. |
| Cycle(주기) | Seasonality는 특정 기간에 정확하게 나타나는 변동성을 갖고 있는 반면, Cycle의 경우 특정 시간에 구애 받지 않습니다. 하지만 동일하게 특정 패턴을 갖고 있습니다. 보통 2~3년처럼 장기간에 걸친 패턴을 갖고 있을수 있습니다. 예를 들어서 business cycle의 경우에는 호황 -> 불황 -> 침체 -> 회복 의 cycle을 갖고 있습니다. |
| Irregularity(불규칙성) | 또는 random variations이라고 불리며 예상치 못한 영향에 의해서 나타납니다. 예를 들어서 전쟁, 지진, 홍수, 혁명등등이 될 수 있습니다. |
Stationary Time Series
다음과 같은 조건을 갖으면 Stationary Time Series라고 할 수 있습니다.
모든 \(t\)에 관하여 일정한 평균
\(E(x_t) = \mu\)
모든 \(t\)에 관하여 일정한 분산
\(E[(x_t - \mu)^2] = Var(x_t) = \sigma^2 = \gamma(0)\)
covariance는 t가 아닌 s에 의존
\(cov(y_t, t_{t+s}) = cov(y_t, y_{t-s}) = \gamma_s\)
즉 평균과 분산이 각각 상수를 갖고 있으며, 시간이 지나도 평균과 분산이 변하지 않는다는 뜻입니다.
Data
아래의 링크에서 데이터를 다운받을 수 있습니다.
Daily minimum temperatures in Melbourne, Australia, 1981-1990
TEST_SIZE = 50
dataframe = pd.read_csv('international-airline-passengers.csv',
names=[ 'passenger'], index_col=0,
skiprows=1)
dataframe.index = pd.to_datetime(dataframe.index)
dataframe = dataframe.astype('float64')
print(dataframe.head())
scaler = MinMaxScaler()
data = scaler.fit_transform(dataframe.values.reshape((-1, 1)))
# Mean Adjusted Time Series
mu = np.mean(data)
data_adjusted = data - mu
train, test = data_adjusted[:-TEST_SIZE], data_adjusted[-TEST_SIZE:]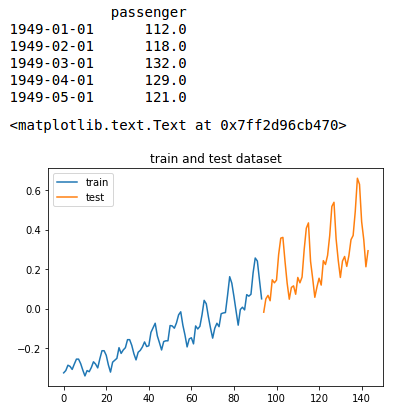
Autocorrelation Checking
Autoregression은 이전의 time-steps의 observations을 통해 다음 step의 값을 예측하는데 사용될 수 있다는 가정을 갖고 있습니다.
variables관의 관계를 correlation이라고 하며, 두 variables이 동시에 증가하거나 감소하면 positive correlation이라고 하며, 서로 반대방향으로 움직인다면 (하나는 증가하고, 하나는 감소하는 상황.) negative correlation이라고 합니다.
output variable (예측값) 그리고 이전 time-steps의 값(lagged variables)들의 correlation을 구함으로서 통계적 측정을 할 수 있습니다.
correlation을 통해서 얼마만큼의 lag variables을 사용해야될지 알 수 있으며, 그래프가 predictable한지 안 한지도 알 수 있습니다.
Autocorrelation에서 auto가 붙는 이유는 위에서 설명했듯이, 자기자신(auto or self)의 데이터를 사용하여 자기 자신의 데이터를 예측하기 때문에 이렇게 이름이 지어졌습니다.
Lag Plot
빠르게 correlation이 존재하는지 확인하는 방법은 step t 와 t-1 을 scatter plot으로 그래서 확인하는 방법입니다.
직접 데이터를 가공해서 만들수도 있지만, Pandas에서는 lag_plot이라는 함수를 통해서 쉽게 lag plot을 그려볼 수 있습니다.
from pandas.plotting import lag_plot
lag_plot(dataframe, lag=1)
title('lag plot')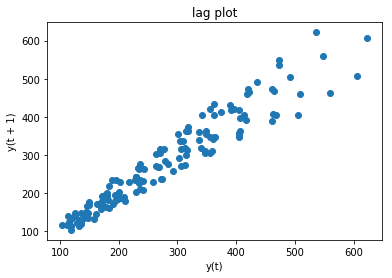
만약 step t 와 step t-1 의 관계가 전혀 없는 random한 상황속에서는 다음과 같이 그래프가 그려집니다.
series = pd.Series([np.random.randint(0, 1000) for _ in range(1000)])
lag_plot(series)
title('random variable lag plot')
Pearson Correlation Coefficient
t-1 과 t의 상관관계를 pearson correlation으로 구할수 있습니다.
- negative correlated: -1
- positive correlated: 1
- correlation: 0.5보다 크거나, -0.5보다 작을시 높은 correlation
아래의 예제에서는 0.77487의 correlation값을 보이는데 positive correlated이며 correlation이 높다고 할 수 있습니다.
from pandas.plotting import autocorrelation_plot
data2 = pd.concat([dataframe.shift(2), dataframe.shift(1), dataframe], axis=1)
data2.columns = ['t-2', 't-1', 't']
data2.corr()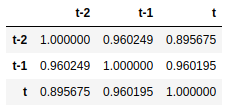
Autocorrelation Plot
각각의 lag variable에 대한 correlation을 plotting할 수 도 있지만, Pandas에서 이미 지원해주고 있습니다.
autocorrelation_plot(data)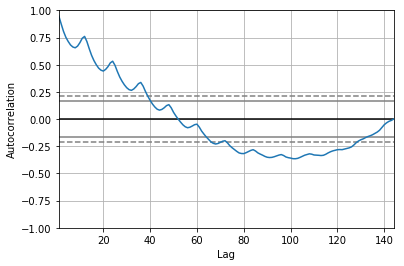
statsmodel 라이브러리에서 제공하는 plot_acf를 사용할수도 있습니다.
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(data, lags=50)
print(end='')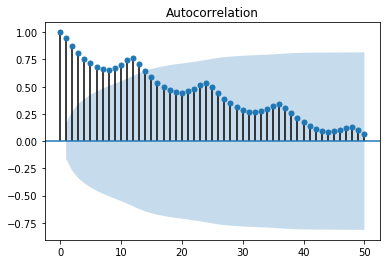
Random variable의 경우에는 다음과 같이 전혀 맞지 않게 나옵니다.
series = pd.Series([np.random.randint(0, 1000) for _ in range(1000)])
plot_acf(series, title='random variable autocorrelation')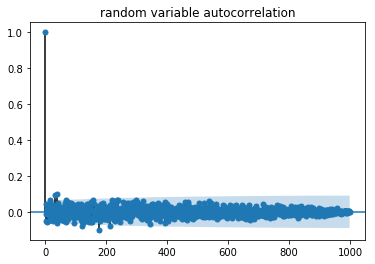
Lag Operator
Lag Operator \(L\) 또는 Backshift \(B\) 로 표현을 하며 시계열상의 과거의 데이터를 설명할때 사용합니다.
\[\begin{align} Ly_t &= y_{t-1} \\ y_t &= Ly_{t+1} \\ \end{align}\]이때 Lag Operator \(L\) 은 여러가지 정수값으로 제곱이 될 수 있습니다.
\[\begin{align} L^ky_t &= y_{t-k} \\ L^{-1}y_t &= y_{t+1} \\ L^2y_t &= y_{t-2} \\ \end{align}\]Lag Polynomials
\(a(L)\) 를 lag polynomials 로 정의한다면 다음과 같습니다.
\[a(L) = a_0 + a_1L + ... + a_pL^p\]위의 공식은 operator로서 사용이 될 수 있습니다.
\[a(L)x_t = a_0x_t + a_1x_{t-1} + .. + a_p x_{t-p}\]lag polynomials는 더하거나 곱하는 연산을 할 수도 있습니다.
예를 들어서 만약 \(a(L) = (1-aL)\) 이고 \(b(L) = (1-bL)\) 이라면
Invert
lag polymials 는 inverted될 수 있습니다.
\[(1-pL)(1-pL)^{-1} = \frac{(1-pL)}{(1-pL)} = 1\]Difference Operator
Time series 분석에서 first difference operator \(\Delta\) 는 lag polynomial의 특별한 케이스입니다.
\[\begin{align} \Delta X_t &= X_t - X_{t-1} \\ \Delta X_t &= (1 - L)X_t \\ \end{align}\]유사하게 second difference operator는 다음과 같습니다.
\[\begin{align} \Delta(\Delta X_t) &= \Delta X_t - \Delta X_{t-1} \\ \Delta^2 X_t &= (1 - L) \Delta X_t \\ \Delta^2 X_t &= (1-L)(1-L) X_t \\ \Delta^2 X_t &= (1-L)^2 X_t \end{align}\]위의 공식은 다음과 같이 일반화 될 수 있습니다.
\[\Delta^i X_i = (1-L)^i X_t\]Seconds Difference의 예제는 다음과 같습니다.
| Original Sequence | 0 | 1 | 4 | 9 | 16 | 25 | 36 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| First Difference | 1 | 3 | 5 | 7 | 9 | 11 | |||||||
| Second Difference | 2 | 2 | 2 | 2 | 2 |
AR (Autoregressive) Model
AR(p) (AutoRegressive of order p)는 간단하게 과거의 패턴이 지속된다면
시계열 데이터 관측치 \(y_t\) 는 과거 관측치 \(y_{t-1}\), \(y_{t-2}\), \(y_{t-3}\), … 에 의해 예측될 수 있다고 봅니다.
오직 과거의 데이터(lagged variables)만 사용해서 예측 모형을 만들게 되며, 이름도 autoregressive 입니다. (그리스어로 auto 라는 뜻은 “self”를 가르킵니다.)
- order: \(p\)
- parameters (coefficients): \(\alpha_1\), \(\alpha_2\), …, \(\alpha_p\)
- error term (white noise): \(\epsilon_t\)
즉 time lag operator를 사용하면 다음과 같이 공식을 세울 수 있습니다.
그리고 아래의 notation은 ARMA (autoregressive moving average)와 동일합니다.
이때 다음과 같은 조건들을 갖습니다.
\[\begin{align} |\alpha| &< 1 \\ Var[X_t] &= \frac{\sigma^2}{1-\sigma^2} \end{align}\][Code] Using StatsModels
statsmodel에서 제공하는 AR 을 사용하면 Autoregressive Model을 구현할 수 있습니다.
문제는 해당 라이브러리가 학습된 부분에서 예측을 하면 잘되나, forecast를 하려고 하면 잘 나오지를 않습니다.
이는 라이브러리가 학습했었던 데이터 자체를 갖고 있고, 이것을 토대로 하여 예측을 하기 때문에, 학습 데이터의 범위를 넘어서 예측을 하려고 하면 잘 되지를 않습니다.
PRED_N = 300
model_ar = AR(train)
model_ar = model_ar.fit(disp=True)
pred_train = model_ar.predict(start=model_ar.k_ar, end=len(train)-1)
pred_test = model_ar.predict(start=len(train), end=len(train)+len(test)-1)
### 생략 ###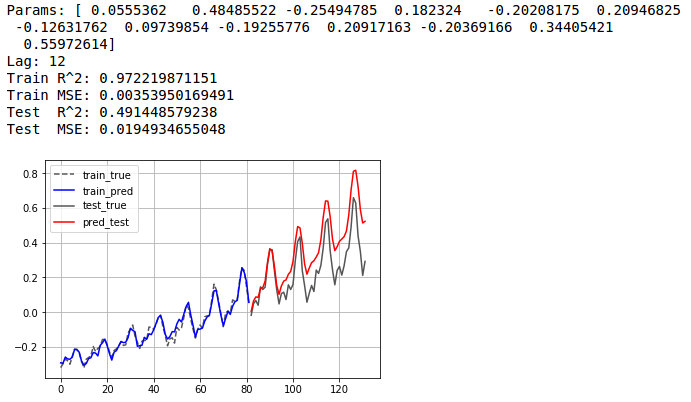
[Code] Using Oridinary Least Square Estimation
ols = sm.OLS(train[LAG+1:], sm.add_constant(ts_train)[:-1], )
ols = ols.fit()
display(ols.summary())
def predict_with_ols(ols, x, length):
h = np.ones(x.shape[0] + 1)
h[1:] = x
response = list()
for _ in range(length):
p = ols.predict(h)
h[1:-1] = h[2:]
h[-1] = p
response.append(p)
response = np.array(response)
return response
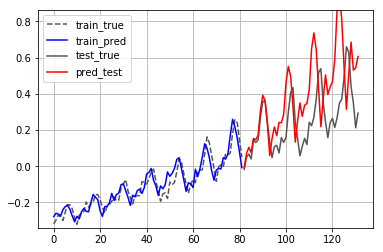
train_pred = ols.predict(sm.add_constant(ts_train))
test_pred = predict_with_ols(ols, ts_train[-1], length=len(test))
show_result(train, test, train_pred, test_pred, lag=LAG)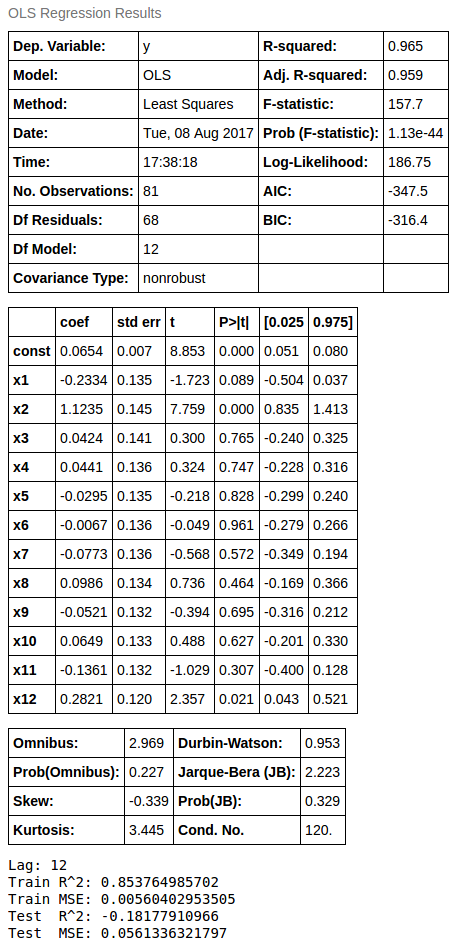
[Code] Using Polynomial Curve Fitting
과거 12개 데이터를 통해서 그 다음을 예측합니다.
LAG = 12
DEGREE = 1
def poly_pred(poly, x, lag, length):
h = x
result = list()
for _ in range(math.ceil(length/lag)):
h = np.polyval(poly, h)
result += h.reshape(-1).tolist()
result = np.array(result[:length])
return result
poly = np.polyfit(train[:-LAG].reshape(-1), train[LAG:].reshape(-1), DEGREE)
train_pred = np.polyval(poly, train[:-LAG])
test_pred = poly_pred(poly, train[-LAG:], lag=LAG, length=len(test)) # np.polyval(poly, train[-LAG:])
show_result(train, test, train_pred, test_pred, lag=LAG)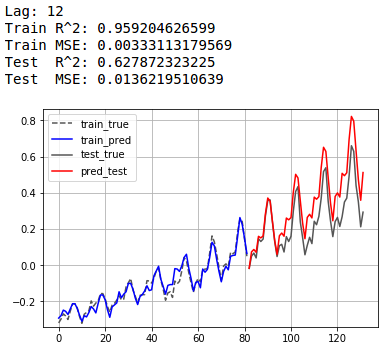
Moving Average Model
Moving-average Model은 univariate time series를 모델링 하는데 사용되는 방법중의 하나입니다.
AR Model과 함께 ARMA 그리고 ARIMA 모델의 중요 컴포넌트가 됩니다.
Moving Average Model은 Moving Average와 전혀 다릅니다.
또한 AR과 다르게 MA는 항상 stationary 입니다.
Definition
Moving Average with orders p and q 모델은 noise에 관하여 \(X_t\)에 대해 다음과 같이 정의를 하고 있습니다.
\[X_t = \epsilon_t + \beta_1 \epsilon_{t-1} + ... + \beta_q \epsilon_{t-q}\]noise 의 (weighted)평균으로 구해지지만 전체 시간을 모두 구하는 것이 아니라, average moving \(t\) 그리고 \(q+1\) times가 사용됩니다.
time lags를 사용하여 다음과 같이 정의 할 수 있습니다.