Likelihood

Likelihood는 unknown parameters \(\theta\) 를 추정한는데 사용되는 함수입니다.
\(X^n = (x_1, ... x_n)\) 는 joint density \(P(x^n;\theta) = p(x_1, ..., x_n; \theta)\) 를 따를때..
likelihood function 은 다음과 같이 정의 될 수 있습니다.

\[L(\theta) = L(\theta; x^n) = P(x^n; \theta)\]

여기서 \(x^n\) 은 parameter로 고정되었으며, \(\theta\) 는 variable입니다.
Likelihood의 몇가지 속성은 다음과 같습니다.

만약 데이터가 iid (identically independent distribution) 이라면 likelihood function은 다음과 같이 정의 됩니다.

\[\begin{align} L(\theta\ |\ x) &= \prod^n_{i=1} p(x_i ; \theta) \\ &= \prod^n_{i=1} L(\theta ; x_i) \end{align}\]

Coin Flipping Example

동전을 independently 10번 동졌을때 앞면이 나올 확률을 계산하려고 합니다.
10번을 던졌을때 HHTHHHTTHH 가 나왔을때 Binomial distribution을 적용했을때 다음과 같습니다.

Bernoulli distribution은 다음과 같으며, \(\theta\) 는 성공확률이라고 보면 됩니다.
\(f(k; \theta) = \theta^k (1-\theta)^{1-k} \qquad x \in \{0, 1\}\)

\[\begin{align} P(data\ |\ \theta) &= P(HHTHHHTTHH\ |\ \theta) \\ &= \theta^{7} (1-\theta)^{10-7} \end{align}\]

이경우 variable data \(x\) 는 이미 수집되어 있으므로 고정되어 있다고 봅니다.
Parameters \(\theta\) 는 원래는 고정된 값이지만 아직 모르는 값입니다.

Probability density function와 Likelihood function 의 차이점은 고정되어 있는 parameters를 서로 뒤바꿔 준다는 것입니다.
예를 들어서 \(f(x\ |\ \theta)\) 였다면 likelihood는 \(f(\theta\ |\ x)\) 로 바꿔줍니다.
(\(x_i\) 는 1이면 head이고 0이면 tail 입니다.)

\[\begin{align} L(\theta\ |\ data) &= P(\theta\ |\ HHTHHHTTHH) \\ &= \prod^n_{i=1} f(x_i; \theta) \\ &= \theta^{x_1} (1-\theta)^{1-x_1} \cdot \theta^{x_2} (1-\theta)^{1-x_2} \cdot ... \cdot \theta^{x_n} \\ &= \theta^{7} (1-\theta)^{10-7} \end{align}\]

Probability distribution function \(P(data\ |\ \theta)\) 와 Likelihoood function 의 결과는 동일합니다.
하지만 그 의미는 매우 다릅니다.

\[L(\theta\ |\ data) = P(data\ |\ \theta)\]

Code

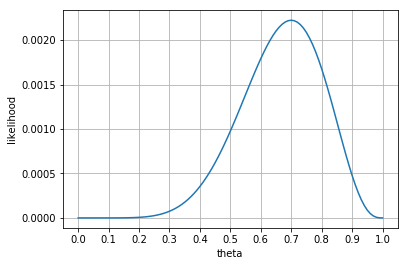
아래의 코드는 서로다른 \(\theta\) 에 따른 likelihood를 계산한 것입니다.

def bernoulli_likelihood(theta):
    return theta**7 * (1-theta)**3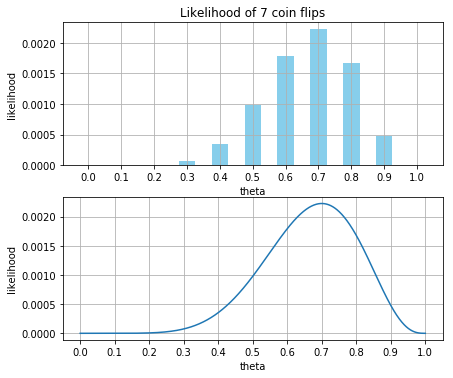

Loglikehood

대부분의 경우에서는 computation의 이유로 log-likelihood 를 사용합니다.

\[l(\theta\ |\ x) = \log L(\theta\ |\ x)\]

예를 들어서 binomial loglikelihood 는 다음과 같습니다.

log rule을 참조합니다.
power rule: \(\log m^r = r( \log m)\)
product rule: \(\log_b(x \cdot y) = \log_b(x) + \log_b(y)\)

\[\begin{align} l(\theta\ |\ x) &= \log \left( \theta^x (1-\theta)^{n-x} \right) \\ &= \log \big(\theta^x \big) + \log \big((1-\theta)^{n-x} \big) \\ &= x \log \theta + (n-x) \log (1-\theta) \end{align}\]

대부분의 문제에서, loglikelihood는 하나의 observation으로 연산하는 것이 아니라 sample로 부터 연산을 합니다.
Independent sample \(x_1, x_2, ..., x_n\) 의 likelihood의 곱은 overall likelihood와 동일합니다.

\(x\) 이나 \(x_i\) 냐를 잘 구분지어서 봐야 합니다.

\[\begin{align} L(\theta\ |\ x) &= \prod^n_{i=1} f(x_i | \theta) \\ &= \prod^n_{i=1} L(\theta\ |\ x_i) \end{align}\]

Log-likelihood의 정의는 다음과 같습니다.

\[\begin{align} l(\theta\ |\ x) &= \log \prod^n_{i=1} f(x_i\ |\ \theta) \\ &= \sum^n_{i=1} \log f(x_i\ |\ \theta) \\ &= \sum^n_{i=1} \log f(\theta\ |\ x_i) \end{align}\]

Maximum Likelihood

간단히 정의하면, 주어진 샘플 \(x\) 에 대해서 likelihood를 maximize하는 parameter \(\theta\) 를 찾는 것입니다.
위의 동전 던지기 예제에서는 0.7 정도가 maximum likelihood로 볼 수 있습니다.
Likelihood function \(\mathbf{L} = f(\mathbf{x};\theta)\) 일때 Maximum likelihood estimator (MLE)의 공식은 다음과 같습니다.

\[\hat{\theta}(x) = arg\max_{\theta} \mathbf{L}(\theta | \mathbf{x})\]

hat을 씌워주는 이유는 estimate이라는 것을 표현하기 위해서 씌워 놓습니다.

Fireman Test Example

\(X^n = (x_i, ..., x_n)\) 샘플이 있으며 다음과 같은 값을 갖을 수 있습니다.

  • \(x_i = 0\) : 소방관 시험에 합격한 사람
  • \(x_i = 1\) : 소방관 시험에 불합격한 사람

\(x_i\) 가 independent Bernoulli random variables이며 parameter \(\theta\) 는 모르고 있을때,
각각의 \(x_i\) 에 대한 Probability mass function 은 다음과 같을 것입니다.

\[f(x_i; \theta) = \theta^{x_i} (1-\theta)^{1-x_i}\]
  • \(\theta\) 는 확률로서 0에서 1의 값을 갖습니다.

따라서 likelihood function \(P(\theta)\) 는 다음과 같을 것입니다.

\[\begin{align} L(\theta) &= \prod^n_{i=1} f(x_i; \theta) \\ &= \theta^{x_1} (1-\theta)^{1-x_1} * \theta^{x_2} (1-\theta)^{1-x_2} * ... * \theta^{x_n} (1-\theta)^{1-x_n} \\ &= \theta^{\sum x_i} (1-\theta)^{n-\sum x_i} \end{align}\]

Likelihood를 알아냈지만, maximum likelihood의 연산량을 줄이기 위해서 log likelihood를 사용합니다.

\[\begin{align} \ln L(\theta) &= \left( \sum^n_{i=1} x_i \right) \ln\theta + \left(n-\sum^n_{i=1} x_i \right) \ln(1-\theta) \\ &= n\big( \bar{x} \ln \theta + (1-\bar{x}) \ln(1-\theta) \big) \end{align}\]

Likelihood를 알아냈으면 maximum likelihood를 partial derivative로 찾을수 있습니다.
이때 derivative의 값은 0으로 놓습니다.

Drivative rule 참고.
\(\frac{d}{dx} \ln(x) = \frac{1}{x}\)
\(\frac{d}{dx} \log_a(x) = \frac{1}{x \ln(a)}\)

\[\begin{align} \frac{\partial}{\partial \theta} \ln L(\theta | \mathbf{x}) &= n\left( \frac{\bar{x}}{\theta} - \frac{1-\bar{x}}{1-\theta} \right) \\ &= n \left( \frac{\bar{x}(1-\theta)}{\theta(1-\theta)} - \frac{\theta(1-\bar{x})}{\theta(1-\theta)} \right) \\ &= n \frac{\bar{x}-\theta}{\theta(1-\theta)} = 0 \end{align}\]

\(n \frac{\bar{x}-\theta}{\theta(1-\theta)}\) 값이 0이 되려면 \(\bar{x} = \theta\) 일 경우에 0이 될 수 있습니다.
따라서 maximum likelihood estimate 은 다음과 같습니다.

\[\hat{\theta}(x) = \bar{x}\]

Code

아래의 코드는 7명이 합격하고, 3명이 실패했을때 입니다. (coin flip과 동일)
계산 방식을 각각의 probability mass function을 구한 다음에 곱으로 \(\prod\) 계산한 것입니다.

def bernoulli_likelihood2(x, theta):
    return theta**x * (1-theta)**(1-x)

theta = np.arange(0, 1.01, 0.01)
x = np.array([1, 1, 1, 1, 1, 1, 1, 0, 0, 0])

p = [np.prod(bernoulli_likelihood2(x, t)) for t in theta]
disply_plot(theta, p)

# Estimate Maxmum Likelihood
maximum_likelihood = float(np.mean(x))
print('Maximum likelihood estimate: ', maximum_likelihood)

Maximum likelihood estimate: 0.7