Linear Regression

Forecasting Numeric Data
수학은 삶의 수많은 관계(Relationships)에 대하여 설명을 해줍니다.
예를 들어, 칼로리 섭취량과 몸무게량.. 연봉과 학벌 또는 경력과의 관계등등..
상식적으로도 먹는게 많은면 몸무게가 많을 것이고, MIT를 나오면 연봉이 더 높겠죠(아마도 구글이나 FB에 있겠죠?)
(ㅎㅎㅎ 참고로.. 제가 가르친 학생중에 페이스북, 구글에 있는 제자들도 있습니다. 청출어람인가? 부럽다!)
물론 Regression을 통해나온 정량화된 측정 수치가 정확한 예측을 한다고 보지는 않습니다.
하지만 평균적인 값을 통해서 대체로 이렇게 되겠지 수치화 할 수는 있겠죠.
개인적으로 실무에서 누군가한테 데이터 뽑아서 보여줄때 정말 많이 사용하는 방법이고..
쉽고 빠르고.. 수학적으로도 전혀 어렵지 않아서 배워두면 누구나 쉽게 할 수 있다고 생각합니다.
(Generalized Linear Models - GLM 즉.. 어떤 데이터에도 general하게 사용 가능한 메소드중의 하나)
Regression의 종류로는 Linear Regression, Logistic Regression, 그리고 Poisson Regression 등등이 있지만.. 일단 가장 기본적인 Linear Regression을 다루도록 하겠습니다.
Sample Data
- Bwt : Body Weight in kilograms
- Hwt : Head Weight in grams
즉.. 고양이의 몸통이 크면 머리도 큰지에 관한 상관관게를 하겠음..
Definitions
| Term | Definition | 쉽게말해 |
|---|---|---|
| Dependent variable | a single numeric value to be predicted | 예측값 |
| Independent variables (predictors) | one or more numerics | 예측을 위해 사용되는 값들 |
y = a + bx
# y -> dependent variable
# x -> independent variable
# a -> y-intercept
# b -> slope우리들의 목표는 가장 최적화된 a, b의 값을 알아내는 것입니다.
R
> cats <- read.csv('cats.csv')
> head(cats)
Sex Bwt Hwt
1 F 2.0 7.0
2 F 2.0 7.4
3 F 2.0 9.5
4 F 2.1 7.2
5 F 2.1 7.3
6 F 2.1 7.6
> lm.out <- lm(Hwt~Bwt, data=cats)
Call:
lm(formula = Hwt ~ Bwt, data = cats)
Coefficients:
(Intercept) Bwt
-0.3567 4.0341
> with(cats, plot(Bwt, Hwt))
> abline(lm.out, color='red')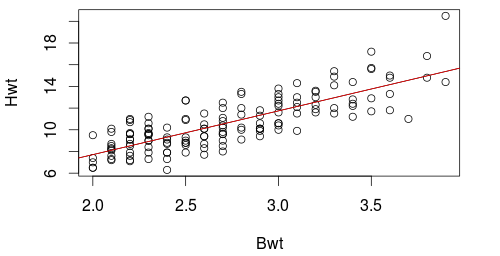
par(mfrow=c(2,2))
> plot(lm.out)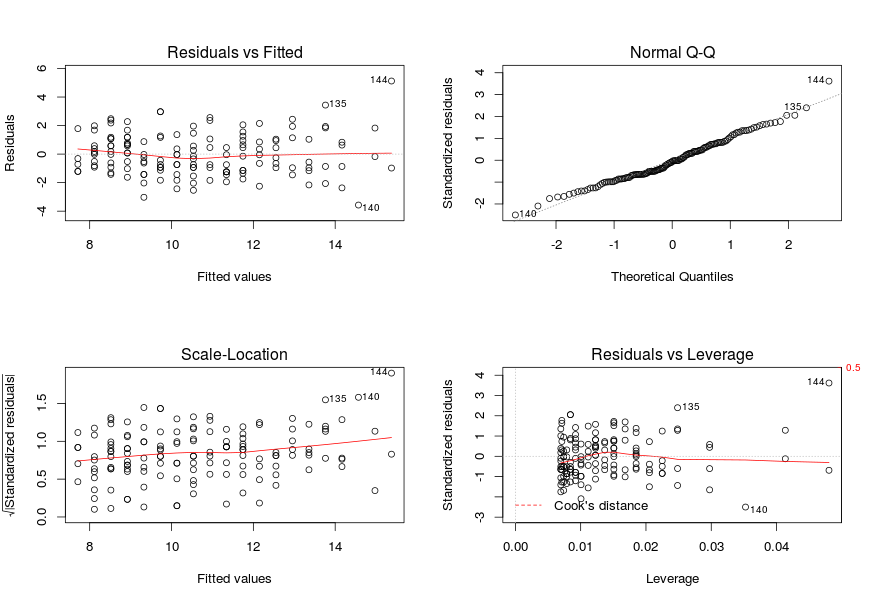
첫번째 plot은 resuduals 과 fitted line과의 관계를 그린 것입니다.
즉.. 저 fitted line과 residuals과의 거리가 멀수로 outliers 가 있다는 뜻이겠죠.
두번째 plot은 normal quantile plot of the residuals 으로서..
residuals 들이 normally distributed 됐는지 보여줍니다.
> cats[144,]
Sex Bwt Hwt
144 M 3.9 20.5
> lm.out$fitted[144]
144
15.37618 144번 고양이가 가장 몸도 크고, 머리도 큰 고양이입니다.
몸통은 3.9kg 이고, 머리는 20.5g 입니다.
fitted value는 15.37618 으로서 residual value는 5.12382 입니다.
> summary(lm.out)
Call:
lm(formula = Hwt ~ Bwt, data = cats)
Residuals:
Min 1Q Median 3Q Max
-3.5694 -0.9634 -0.0921 1.0426 5.1238
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.3567 0.6923 -0.515 0.607
Bwt 4.0341 0.2503 16.119 <2e-16 ***
Residual standard error: 1.452 on 142 degrees of freedom
Multiple R-squared: 0.6466, Adjusted R-squared: 0.6441
F-statistic: 259.8 on 1 and 142 DF, p-value: < 2.2e-16summary를 보니.. Residual standard error: 1.452 로 나옵니다.
144번 고양이의 residual value 5.12382 를 standardized residual 로 변화시키면 ..
> 5.12382/1.452
3.5288016528925623> par(mfrow=c(1,1))
> plot(cooks.distance(lm.out))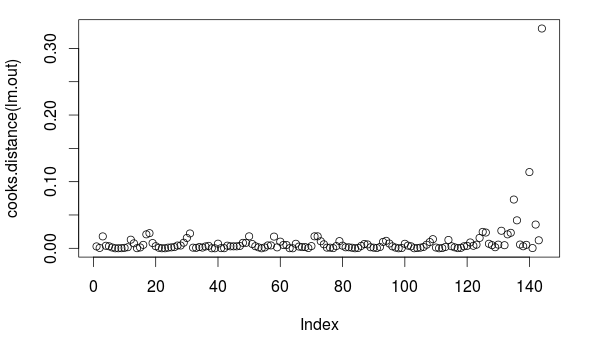
cooks distance plot에서 보듯이 144번은 outlier입니다.
Formula
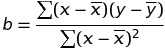
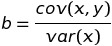
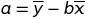
sample data였던 cats의 Linear Regression.
Coefficients:
(Intercept) Bwt
-0.3567 4.0341 Python Pandas를 사용해서 a 와 b값을 찾도록 해보겠습니다.
import pandas as pd
cats = pd.read_csv('cats.csv')
slope = (sum((cats['Bwt'] - cats['Bwt'].mean()) *
(cats['Hwt'] - cats['Hwt'].mean())) /
sum((cats['Bwt'] - cats['Bwt'].mean()) ** 2))
# 4.03406269846
slope = cats['Bwt'].cov(cats['Hwt']) / cats['Bwt'].var()
# 4.03406269846
intercept = cats['Hwt'].mean() - slope * cats['Bwt'].mean()
# -0.356662432885Python
import pandas as pd
from pandas.stats.api import ols
cats = pd.read_csv('cats.csv')
ols(y=cats['Hwt'], x=cats['Bwt'])
#-------------------------Summary of Regression Analysis-------------------------
#
# Formula: Y ~ <x> + <intercept>
#
# Number of Observations: 144
# Number of Degrees of Freedom: 2
#
# R-squared: 0.6466
# Adj R-squared: 0.6441
#
# Rmse: 1.4524
#
# F-stat (1, 142): 259.8348, p-value: 0.0000
#
# Degrees of Freedom: model 1, resid 142
#
# -----------------------Summary of Estimated Coefficients------------------------
# Variable Coef Std Err t-stat p-value CI 2.5% CI 97.5%
# --------------------------------------------------------------------------------
# x 4.0341 0.2503 16.12 0.0000 3.5436 4.5246
# intercept -0.3567 0.6923 -0.52 0.6072 -1.7135 1.0002
# ---------------------------------End of Summary---------------------------------