Monty Hall Problem - Bayes

당신은 전날밤 술에 취했고 깨어나보니 어두운 방에 갖혀 있었다.
흐릿했던 초점이 돌아오고 정신이 드니 눈앞에 직소가 있었고 옆에는 3개의 문이 있다.
그리고 직소는 당신과 게임을 하길 원한다.
게임의 룰은 다음과 같다.
- 3개의 문이 있다.
- 단 하나의 문 뒤에 살아나갈수 있는 열쇠가 있다.
- 게임의 시작은 당신이 먼저 열쇠가 있을거 같은 문을 선택을 한다. (선택만하고 문은 열지 않는다)
- 직소는 선택하지 않은 문 2개중에 열쇠가 없는 문을 연다. (즉 직소는 당연히 열쇠가 어디 있는지 알고 있다.)
- 그리고 당신에게 선택이 주어진다. 처음에 선택한 문을 열것인가? 아니면 결정을 바꾸고 다른 문을 선택할 것인가?
- 열쇠가 있는 문을 선택하면 살고, 뒤에 아무것도 없으면 죽는거임
자.. 먼저 아래의 내용을 보시기 전에 당신의 선택은 어떻게 하시겠습니까?
또 그렇게 결정한 이유가 무었입니까?
Conditional Probability
보통 2개의 이벤트(상황)이 있는데 서로 영향을 미치는(dependent) 상황일때 사용을 합니다. 예를 들어서 담배를 많이 필수록 폐암에 걸릴 확률이라든가, 오늘 비가온다면 내일 비가 올 확률이 좀 더 높다든가.. 하여튼 어떠한 이벤트의 경우에 따라서 다른 이벤트에 영향을 주는 경우에 Conditional Probability 사용이 가능합니다.
다음은 그냥 몇가지 공식을 적어드립니다.
그냥 묻지도 따지지도 말고 그냥 왜우면 되요 :) (이런걸 Axiom이라고 하죠..)
- A라는 이벤트가 일어날 확률은 P(A) 이렇게 적습니다.
ex) P(head) 동전의 앞면이 나올 확률 - 그런데 B라는 조건하에 A라는 이벤트가 일어날 확률은 P(A|B) 이렇게 적습니다.
ex) P(암|담배) 담배를 피울때 암에 걸릴 확률 - P(A and B) = P(A)P(B|A)
A 와 B는 dependent 이며 A 그리고 B 가 동시에 일어날 경우..
참고로 A 와 B 가 independent라면 P(A)P(B) 로 표현될수 있습니다.
가령 동전 A가 앞면이고, 동전 B가 앞면일 확률
0.5 * 0.5 = 0.25 - P(A and B) = P(B and A)
그런데 말입니다?!

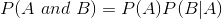
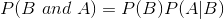
따라서..
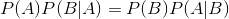
즉 서로 바꿔 쓸수 있으며 아주 중요한 내용이다. 여기서 조금더 나가면.. 바로.. 그 유명한 Bayes Formula 를 얻을수 있다.
=====================================
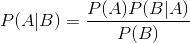 =====================================
=====================================
위의 공식을 통해서 직소 문제를 풀어보도록 하겠습니다.
Bayes라고 쓰는 이유는 그냥 옛날 옛적에 베이즈라는 사람이 만들어서 그 사람 이름 딴 거임 ..
Monty Hall Problem
여름이라서 직소를 내보냈는데.. 사실 이 문제는 Monty Hall Problem이라고 해서 실제 외국 TV쇼에서 했었던 문제입니다. 궁금하면 직접 찾아보시길.. 다른게 있다면 3개중에 한개에는 “자동차”같이 짱짱맨 선물이 있다는거
당시에 학계? 에서는 이 Monty Hall Problem으로 논란?이 된 적도 있었습니다. 실제 당시의 저명한 교수가 TV에 출연해서.. 처음 선택한걸 열거나 또는 바꾸거나 확률은 그게 그거다 라고 아주 열띄게 강조도 했었을 정도였으니…
상식적으로 생각하면.. 어차피 3개의 문에 랜덤으로 키가 있는거고.. 나는 그 랜덤 중에서 고르는 것인데.. 처음걸 선택하거나 또는 원래 선택에서 바꾸는게 그렇게 큰 의미가 있을까? 생각이 들 수도 있습니다.
자.. 위에서 배운 Bayes 공식으로 문제를 풀어보도록 하겠습니다.
대충 상황은 다음과 같다고 가정을 하겠습니다.
- 문 A, B, C 가 있다.
- 당신은 A문을 최초로 선택을 했다. (문은 열지 않았다.)
- 직소는 B의 문을 열었고, B문의 뒤에는 아무것도 없었다. (직소는 어디에 열쇠가 있는지 알고 있다.)
첫번째 이벤트 P(Jigsaw Opens B)는 직소가 문 B를 열었다는 것이고..
두번째 이벤트 P(Key@..) 는 여러분이 어디 문을 열었을때의 확률입니다.
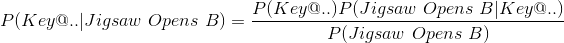
| P(key@..) | P(jigsaw Opens B|Key@..) | P(Key@..)P(jigsaw Opens B|Key@..) | |
|---|---|---|---|
| A문 | P(key@A) = 1/3 | P(jigsaw Opens B|Key@A) = 1/2 | 1/3 * 1/2 = 1/6 |
| B문 | P(key@B) = 1/3 | P(jigsaw Opens B|Key@B) = 0 | 1/3 * 0 = 0 |
| C문 | P(key@C) = 1/3 | P(jigsaw Opens B|Key@C) = 1 | 1/3 * 1 = 1/3 |
공식에 따르면 P(Jigsaw Opens B) 의 확률을 구해야 하는데 어차피 하나마나라서 안해도 됩니다.
참고로 P(Jigsaw Opens B)의 값은 1/2 입니다. 당신이 문을 선택하고, Jigsaw가 선택할수 있는 문의 확률
- P(Key@A) 라는 뜻은 A의 문을 열 확률입니다.
- P(Jigsaw Opens B|Key@B) 라는 뜻은 키가 B에 있을때, 직소가 B를 열 확률인데.. 당연히 B에 있는데 열리가 없겠죠
결론적으로 키가 A에 있을 확률은 1/6 이고, C에 있을 확률은 1/3입니다.
즉 2배 차이가 나며 베이즈 확률에 따르면, 원래 선택했던거 말고 바꾸는 것이 살아날 확률을 2배 정도 높입니다
아래의 동영상을 보시면.. 중간쯤에 실제로 실험을 합니다.
검을색 옷을 입은 남자는 자기가 최초에 선택한 컵을 선택하고 기회가 주어졌을때 바꾸지 않습니다.
빨간색 옷을 입은 남자는 기회가 주어졌을때 무조건 다른것을 선택합니다.
실제 실험을 했을때 검을색 옷의 남자는 2대의 자동차밖에 못 얻었지만, 빨간색 옷 남자는 16대의 자동차를 얻습니다.
뭐 2배 이상을 훨씬 뛰어 넘었네요..
자.. 그래서 결론은..
데이터 사이언티스트들이 이런 Bayes 확률로 어떻게 뭘 할건데? 이런거인데요..
이거는 언젠가 시간이 나면 다루도록 하겠습니다.
실무에서는 주로 Text Classification 에서 활용이 되고 있습니다.
다른 Machine Learning 알고리즘보다 복잡하지 않으면서 강력하게 활용이 될 수 있습니다.