Momentum

CS231n Convolutional Neural Networks for Visual Recognition

Data

data = np.loadtxt('../../data/linear-regression/ex1data1.txt', delimiter=',')
X = data[:, 0].reshape(data[:, 0].shape[0], 1) # Population
Y = data[:, 1].reshape(data[:, 1].shape[0], 1) # profit

# Standardization
scaler_x = StandardScaler()
scaler_y = StandardScaler()
X = scaler_x.fit_transform(X)
Y = scaler_y.fit_transform(Y)

scatter(X, Y)
title('Profits distribution')
xlabel('Population of City in 10,000s')
ylabel('Profit in $10,000s')
grid()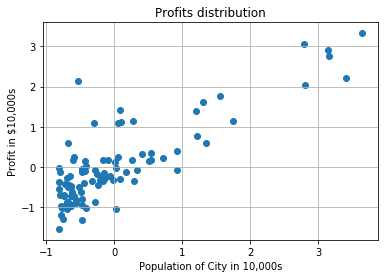

Momentum Update

물리학적인 관점에서 optimization problem을 바라봤을때, convergence rate를 향상시킬수 있는 방법이 있습니다.
Loss를 산등성이에서 height로 바라봤을때 물리학적으로 potential energy를 갖을수 있게 됩니다.) (TODO:추가 연구 필요)

negative gradient는 양옆 가파른 산골짜기의 한쪽을 타고 조금씩 내려오는 형태와 유사하기 때문에 SGD는 convergence까지 매우 느립니다. (특히 초기 steep gain이후에 계속해서 더 느려짐)

\[\begin{align} v &= \gamma v_{t-1} + \eta \nabla_{\theta} J(\theta; x^{(i)},y^{(i)}) \\ \theta &= \theta - v \end{align}\]

위의 SGD예제처럼 gradient값이 직접적으로 weights에 영향을 주는것이 아니라, gradient값은 오직 velocity에 영향을 주게 됩니다.
그 뒤 velocity는 weights값에 영향을 미치게 됩니다.

코드에서 구현은 안되어 있지만 일반적으로 momentum은 0.5에서 시작해서 끝날때쯤에는 0.99까지 가게 만드는게 일반적입니다

w = np.array([-0.1941133,  -2.07505268])

def predict(w, X):
    N = len(X)
    yhat = w[1:].dot(X.T) + w[0]
    yhat = yhat.reshape(X.shape)
    return yhat

def momentum_nn(X, Y, w, eta=0.1, gamma=0.5):
    N = len(X)
    v = np.zeros(w.shape[1:])
    v_b = np.zeros(1)

    for i in range(N):
        x = X[i]
        y = Y[i]
        yhat = predict(w, x)
        delta = y - yhat

        v = gamma*v + 2/N * eta * np.sum(-delta.dot(x))
        v_b = gamma*v_b + 2/N * eta * np.sum(-delta)

        w[1:] = w[1:] - v
        w[0] = w[0] - v_b
    return w


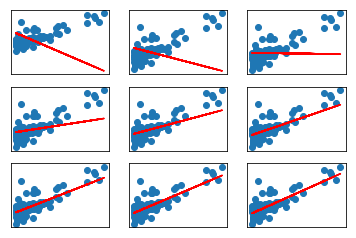
for i in range(1, 10):
    w = momentum_nn(X, Y, w)
    yhat = predict(w, X)

    axes = subplot(3, 3, i)
    axes.get_xaxis().set_visible(False)
    axes.get_yaxis().set_visible(False)

    scatter(X, Y)
    plot(X, yhat, color='red')

    yhats = np.where(yhat >= 0.5, 1, 0)
    accuracy = mean_squared_error(Y, yhats)
    print('Mean Squared Error (less is good):', accuracy)

Mean Squared Error (less is good): 1.76244027984
Mean Squared Error (less is good): 1.0
Mean Squared Error (less is good): 1.0
Mean Squared Error (less is good): 0.725250038743
Mean Squared Error (less is good): 0.637070721578
Mean Squared Error (less is good): 0.637070721578
Mean Squared Error (less is good): 0.651252102667
Mean Squared Error (less is good): 0.651252102667
Mean Squared Error (less is good): 0.657019385081