Hypothesis Test
1. Hypothesis Test
1.1 Terms
| Name | English | Symbol | Description |
|---|---|---|---|
| 유의수준 | Significance Level | \(\alpha\) | 통계적 가설검정에 사용되는 기준값으로, 95%의 신뢰도를 기준으로 한다면 (1-0.95)인 0.05를 유의수준값으로 사용한다 |
| 유의확률 | Significance probability | p-value |
1.2 귀무가설과 대립가설
- Null Hypothesis \(H_0\) (귀무가설)
- sampling에서는 sample observations은 단순히 우연히 일어난 것이라고 가정함
- 두집단을 비교시 같거나 차이가 없다로 해석을 한다
- 기본적으로는 참으로 추정되며, 거부하기 위해서는 증거가 필요하다
- 예제
- 신약: 신약이 효과가 없다 (일단 기본값)
- 키: 샘플의 평균은 모 평균과 동일하다
- Alternative Hypothesis \(H_1\) or \(H_a\) (대립가설)
- sampling에서는 sample observations은 우연히 일어난 것이 아니라고 가정함
- 두집단을 비교시 차이가 있다고 가정을 한다
- 예제
- 신약: 신약이 효과가 있다
- 키: 샘플의 평균은 모 평균과 다르다
1.3 단측 및 양측 검정
- Two-Tailed Test 양측 검정 -> 다르냐?
- 모집단의 모수가 귀무 가설에서의 값보다 크거나 작은지를 판단하려면
양측 대립 가설을 사용 - 특정 고등학교의 시험 결과가 국가 평균(72점)과
다른지여부를 판단하려고 함
귀무가설은 \(H_0: \mu = 72\) 이고, 대립가설은 \(H_1: \mu \ne 72\)
국가 평균과다른지를 판단하는 것이기 때문에 양측 검정이다. (더 높을수도 더 낮을 수도 있다)
- 모집단의 모수가 귀무 가설에서의 값보다 크거나 작은지를 판단하려면
- One-Tailed Test 단측 검정 -> 보다 크냐 또는 보다 작냐?
- 특정 방향으로 모집단 모수가 귀무가설에서의 값과 다른지 여부를 확인하려면
단측 대립 가설을 사용 - 특정 고등학교의 시험 결과가 국가 평균(72점)보다 더 높은지를 판단하려고 함
귀무가설은 \(H_0: \mu = 72\) 이고, 대립가설은 \(H_1: \mu > 72\)
국가 평균보다높은지를 판단하는 것이기 때문에 단측 검정을 한다
- 특정 방향으로 모집단 모수가 귀무가설에서의 값과 다른지 여부를 확인하려면
2. 제 1종 오류 VS 제 2종 오류
| Decision | \(H_0\) is True (귀무가설 참) | \(H_0\) is not True (귀무가설 거짓) |
|---|---|---|
| Accept \(H_0\) (귀무가설 채택) | Correct (No Error) \(p = 1 - \alpha\) |
Type 2 Error (\(p = \beta\)) 2종 오류 |
| Reject \(H_0\) (귀무가설 기각) | Type 1 Error (\(p = \alpha\)) 1종 오류 |
Correct (No Error) \(p = 1 - \beta\) |
2.1 제 1종 오류 (False Positive)
1종 오류는 귀무가설이 참인데 기각되었을때 발생합니다.
- 1종 오류 확률의 최대 허용치인
유의수준의 기준에 따라서 정해짐 (보통 0.05) 귀무가설을 잘못 기각시킬 확률- 10% 또는 20% 라는 것은 귀무가설을 잘못 기각 시킬 확률이 높아진다는 뜻
- 1% 또는 3% 라는 것은 귀무가설을 잘못 기각 시킬 확률이 낮아진다는 뜻
귀무가설을 지지하는 정도의 확률- 10% 또는 20% 라는 것은 귀무가설을 지지하는 확률이 높다는 뜻
- 1% 또는 3% 라는 것은 귀무가설을 지지하는 확률이 낮다는 뜻
2.2 제 2종 오류 (False Negative)
2종 오류는 귀무가설이 거짓인데, 기각시키지 못했을때 발생합니다.
- 양치기 소년에서 귀무가설은 “늑대가 없다” 입니다. 이때 실제로는 늑대가 있는 케이스 입니다.
그리고 양치기 소년은 늑대가 없다고 말하고 (귀무가설이 맞다!) 다른데 놀러간 케이스라고 할 수 있습니다. - 바이러스 백신을 만들었습니다. 귀무가설은 바이러스 백신은 효과가 없다 입니다.
이때 실제로는 백신이 효과가 있는데도 불구하고 잘못된 판단으로 효과가 없다고 했을때 (귀무가설을 인정) 많은 사람들을 살릴수 있었음에도 불구하고 인명피해를 내놓은 상황일수 있습니다.
2.4 적절한 유의수준과 검정력을 선택
예를 들어 2개의 약품이 있었고 다음과 같은 1종 오류 또는 2종 오류를 범할 수 있습니다.
- 1종 오류: 두개의 약의 효과는 동일하다는 결론 (사실은 다르다) -> 틀려도 기존 제품을 먹으니 크게 문제는 없으나.. 더 좋은 약을 놓치게 되는 경우 문제가 생길수 있다
- 2종 오류: 두개의 약이 효과가 다르다는 결론 (사실은 동일하다)
2.5 알파와 베타를 동시에 줄이는건 불가능
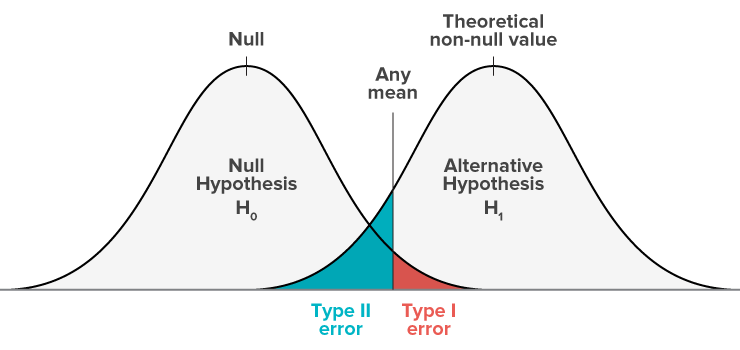
위의 그림에서 보듯이, \(\alpha\) 와 \(\beta\) 를 모두 줄일수는 없습니다.
검사의 신뢰도를 높이기 위해서 임계값을 높여서 (ex. 0.05 -> 0.03) \(\alpha\) 의 범위를 줄이게 되면,
동시에 \(\beta\) 의 범위는 높아지게 됩니다.
즉, \(\alpha\) 와 \(\beta\) 는 서로 상반된 크기를 갖습니다.
2.6 P-Value
- 1종 오류 == p-value (일단 쉽게 이해)
귀무가설을 잘못 기각시킬 확률(정확히는 틀린말이나 쉽게 이해하기 위해)- 오해에 대한 정정
- 귀무가설이 참일 확률은 구할 수 없다 (샘플링 데이터이기 때문에 부정확하게 보는게 맞다)
- p-value는 귀무가설을 잘못 기각시킬 확률이다 라는 말은 부정확하다.
결국 1종 오류를 p-value로 보는 수식에서부터 오는 오해인데,
바로 위에 써놨듯이 귀무가설이 참일 확률을 구할 수 없으며,
따라서 잘못 기각시킬 확률또한 구할 수 없다.
생각해보자.. 샘플링에서 추출한 값이다. ground-truth 값은 모른다
- 앤더슨의 조언
- 실무에서 지나치게 p-value 값에만 의존해서 의사결정을 내리지 않는다. 결국 샘플이고 해당 테스트에만 해당이 된다.
- 다양한 통계 지표와 함께 봐야 하며, 반드시 신뢰구간도 체크를 해야 한다.
- 무조건 0.05 아래면 통과이고, 이상이면 탈락인 상황으로 보지 말자.
특히 서비스의 AB테스트에서 참고 지표로 봐야지 항상 0.05 를 기준으로 판단해서는 안됨 - 결국 샘플에서 만들어진 통계치이다.
P-value (또는 유의 확률 - significance probability)는 바로 1종 오류가 일어날 확률을 의미하고, 일반적으로 5%로 제약을 합니다. (p-value < 0.05)
귀무가설이 맞다고 가정을 할때, 관측된 값보다 극단적인 결과가 실제로 관측될 확률입니다.
예를 들어, 유의수준이 0.05이고, p < 0.03 이라고 할때,
100번의 실험중에 97번의 실험이 연구자의 가설대로 재현이 되었고, 3번째 예외적 경우가 있었다 라고 해석할수 있습니다.
2가지 방식으로 귀무가설을 검증할수 있습니다.
먼저 ppf(1-critical value) 사용해서 검정한는 방법은 다음과 같습니다.
- if abs(statistic) <= critical value: 귀무가설을 채택하며, 평균값을 동일하다
- if abs(statistic) > critical value: 귀무가설을 기각하며, 평균은 서로 다르다
Cumulative distribution function (CDF)를 사용해서 p-value를 구한다음, 유의 수준 \(\alpha\) 와 비교할수도 있습니다.
- if p-value > alpha: 귀무가설을 채택하며, 평균값을 동일하다
- if p-value <= alpha: 귀무가설을 기각하며, 평균값은 서로 다르다
3. Normality Test
-
현실에서는 바빠서 대충 t-test돌리고 하지만, 사실 통계라는 것은 상당히 많은 제약사항들이 붙어 있습니다.
이때 데이터는 정규분포를 따라야 한다와 같은 문장이 있다면 정규성 검증을 통해서 정규분포를 따르는지 먼저 체크를 해줘야 합니다. - 예를 들어 T-test, ANOVA 처럼 모수적 검정방법은 일반적으로 분포가 정규분포를 따른다고 가정을 합니다.
표본의 크기가 30개 이상이 되면 중심극한 정리에 의해서 정규성을 갖고 있다고 가정을 할수 있지만,
30개 미만인 경우에는 정규성 검정을 먼저 수행해야 합니다. 3- 사실 실무에서는 데이터가 대부분 빅데이터라, 이런거 잘 안합니다. - 즉, 표본의 갯수가 10개~30개라면, 정규성 검정이 반드시 필요합니다.
정규성 검정을 통과하면 모수적 검정을 사용해도 되지만, 실패하면 비모수적 검정을 사용해야 합니다. - 만약 표본의 갯수가 30개 이상이라면, 그냥 모수적 검정을 사용해도 됩니다.
3.1 Parametric Test
- 표본의 갯수가 30개 이상이면 parametric test (모수적 검정)을 하면 됩니다.
- 표본의 갯수가 10개이상 30개 미만이면서, 정규성 검정을 통과한다면 모수적 검정을 사용할수 있습니다. (실패하면 비모수적 검정사용)
- 표본의 갯수가 10개미만이라면 non-parametric test (비모수적 검정)을 진행합니다.
3.2 Normal Quantile-Quantile Plot
- 분위수-분위수 그래프
- 정규분포를 따를 경우 일직선으로 나온다
import statsmodels.api as sm
uniform = np.random.random(size=100) * 3.5 + 120
normal = np.random.normal(loc=120, scale=1, size=100)
fig, plots = subplots(1, 2, figsize=(12, 4))
g1 = sm.qqplot(uniform, ax=plots[0])
g2 = sm.qqplot(normal, ax=plots[1])
plots[0].title.set_text('Uniform')
plots[1].title.set_text('Normal')
plt.show()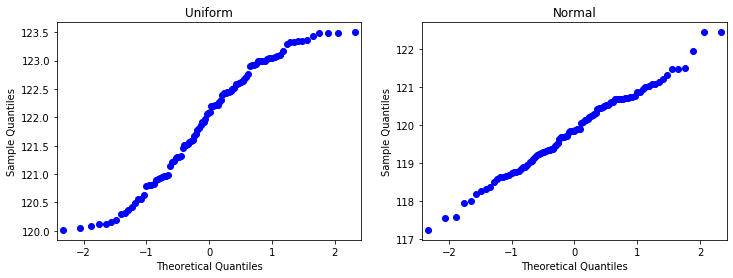
3.3 Histogram
uniform = np.random.random(size=100) * 3.5 + 120
normal = np.random.normal(loc=120, scale=1, size=100)
sns.distplot(uniform, bins=10, label='uniform')
sns.distplot(normal, bins=10, label='normal')
legend()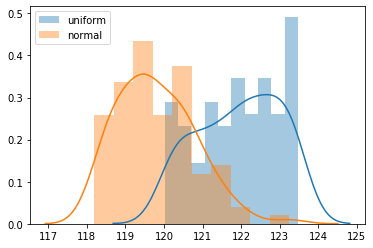
3.4 Shapiro-Wilks Test
- 샤피로 윌크 검정
- 각 샘플안의 관측치는 독립 동일 분포를 따른다 (independetn and identically distributed - iid)
- 표본수가 약 50개 이상 2000개 미만인 데이터셋에 적합 (2000개 이상인 경우 Kolmogorov-Smirnova test 사용)
- 샤피로는 꽤 보수적이기 때문에 히스토그램, 분위수 그래프 함께 사용 권장
- \(H_0\) : 귀무가설은 정규분포를 따른다
- P-value 가 0.05보다 높다면 정규분포를 따른다고 가정한다 (이후 t-test 가능)
from scipy.stats import shapiro
uniform = np.random.random(size=100) * 3.5 + 120
normal = np.random.normal(loc=120, scale=1, size=100)
stat1, p1 = shapiro(uniform)
stat2, p2 = shapiro(normal)
print(f'uniform data | 통계치: {stat1:.2f} | p-value:{p1:.5f} | 정규분포?: {p1 > 0.05}')
print(f'normal data | 통계치: {stat2:.2f} | p-value:{p2:.5f} | 정규분포?: {p2 > 0.05}')
sns.distplot(uniform, label='uniform')
sns.distplot(normal, label='normal')
legend()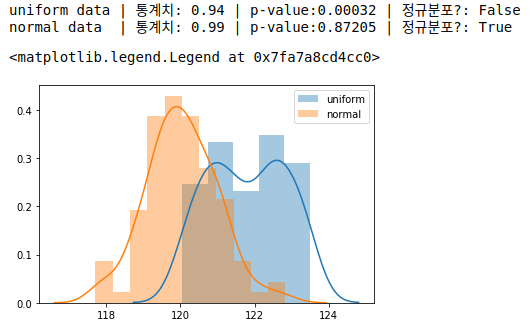
3.5 D’Agostino’s K^2 Test
- 디아고스티노 검정
- 각 샘플안의 관측치는 독립 동일 분포를 따른다 (independetn and identically distributed - iid)
- \(H_0\): 귀무가설은 정규분포를 따른다
- \(H_1\): 대립가설은 정규분포를 따르지 않는다
from scipy.stats import normaltest
uniform = np.random.random(size=100) * 3.5 + 120
normal = np.random.normal(loc=120, scale=1, size=100)
stat1, p1 = normaltest(uniform)
stat2, p2 = normaltest(normal)
print(f'uniform data | 통계치: {stat1:.2f} | p-value:{p1:.5f} | 정규분포?: {p1 > 0.05}')
print(f'normal data | 통계치: {stat2:.2f} | p-value:{p2:.5f} | 정규분포?: {p2 > 0.05}')uniform data | 통계치: 29.70 | p-value:0.00000 | 정규분포?: False
normal data | 통계치: 1.85 | p-value:0.39570 | 정규분포?: True3.6 Anderson-Darling Test
- 각 샘플안의 관측치는 독립 동일 분포를 따른다 (independetn and identically distributed - iid)
- \(H_0\): 귀무가설은 정규분포를 따른다
- \(H_1\): 대립가설은 정규분포를 따르지 않는다
from scipy.stats import anderson
uniform = np.random.random(size=100) * 3.5 + 120
normal = np.random.normal(loc=120, scale=1, size=100)
r1 = anderson(uniform)
r2 = anderson(normal)
print(f'[r1] statistic:{r1.statistic:5.2f} | significance_level: {r1.significance_level}')
print(f'[r2] statistic:{r2.statistic:5.2f} | significance_level: {r2.significance_level}')[r1] statistic: 1.46 | significance_level: [15. 10. 5. 2.5 1. ]
[r2] statistic: 0.74 | significance_level: [15. 10. 5. 2.5 1. ]4. T-Test
- 모집단의 표준편차 \(\sigma\) 를 모를때 사용. (표준오차 \(\frac{s}{\sqrt{n}}\) 를 대신 사용)
- 2개의 집단에 대한 평균의 차이를 검정한다 (3개 이상인 경우 ANOVA 검정을 한다)
- 종속 변수는 continuous variable이어야 한다.
- 관측치는 모두 독립적이어야 한다
- outlier 제거 필수
4.1 One-Sample T-Test
- 단일표본 T 검정
- 표본이 하나일 때, 모집단의 평균과 표본집단의 평균 사이에 차이가 있는지 검정한다
(사실 여기서 모집단은 어떤 값과 비교한다고 생각해도 된다 - ex. 전년도 판매 평균가와 금년도 판매 평균가) - \(H_0: u_0 = u_1\) : 귀무가설은 두 그룹의 평균의 차이는 없다
- \(H_1\) : 대립가설은 one-tail 이냐 또는 two-tail 이냐에 따라서 달라집니다.
- one-tail: \(H_1: u_0 > u_1\) 또는 \(H_1: u_0 < u_1\)
- two-tail: \(H_1: u_0 \ne u_1\)
공식은 아래와 같습니다.
\[t = \frac{\bar{x} - \mu}{\frac{s}{\sqrt{n}}}\]degrees of freedom은 다음과 같습니다.
\[\text{df} = n-1\]4.1.1 Scipy
scipy에서는 ttest_1samp 함수를 사용할 수 있습니다.
다만 ttest_1samp 함수는 two-tailed test입니다.
따라서 one-tailed test를 사용하기 위해서는 p-value값을 2로 나눠줘야 합니다.
scipy.stats.ttest_1samp
This is a two-sided test for the null hypothesis that the expected value (mean) of a sample of independent observations a is equal to the given population mean, popmean.
from scipy.stats import ttest_1samp
np.random.seed(2083)
# Population mean: 100
# 아래는 samples들
sample1 = np.random.normal(loc=98, scale=10, size=500) # 모수보다 -2
sample2 = np.random.normal(loc=99, scale=10, size=500) # 모수보다 -1
sample3 = np.random.normal(loc=100, scale=10, size=500) # 비교되는 모수
sample4 = np.random.normal(loc=101, scale=10, size=500) # 모수보다 +1
sample5 = np.random.normal(loc=102, scale=10, size=500) # 모수보다 +2
# ttest_1samp 는 two-tailed t-test를 진행한다
# 나중에 pvalue/2 를 해줘서 -> one-tailed t-test로 만들어야 한다
t1 = ttest_1samp(sample1, 100)
t2 = ttest_1samp(sample2, 100)
t3 = ttest_1samp(sample3, 100)
t4 = ttest_1samp(sample4, 100)
t5 = ttest_1samp(sample5, 100)
# Visualization
data = [[100, sample1.mean(), sample1.std(), t1.statistic, t1.pvalue],
[100, sample2.mean(), sample2.std(), t2.statistic, t2.pvalue],
[100, sample3.mean(), sample3.std(), t3.statistic, t3.pvalue],
[100, sample4.mean(), sample4.std(), t4.statistic, t4.pvalue],
[100, sample5.mean(), sample5.std(), t5.statistic, t5.pvalue]]
data = pd.DataFrame(data, columns=['p_mean', 's_mean', 's_std', 't-statistic', 'p-value'])
data['less_than'] = data.apply(lambda c: (c['p-value']/2 < 0.05) & (c['t-statistic'] < 0), axis=1)
data['more_than'] = data.apply(lambda c: (c['p-value']/2 < 0.05) & (c['t-statistic'] > 0), axis=1)
data['reject_H0'] = data.apply(lambda c: (c['p-value'] < 0.05) , axis=1)
data = data.round(6)
data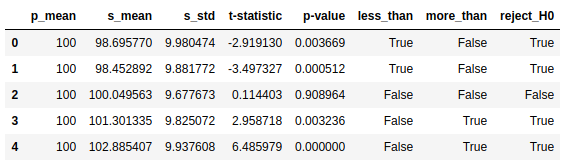
4.1.2 직접 만들어서 사용
- critical value: t.ppf 사용하며, (CDF값을 -> x값으로 변환.
t.ppf(0.95, 10) = 1.812) - p-value: t.cdf(abs(t_statistic), df) 사용
from scipy.stats import t
def my_ttest_1sample(x, population_mean, alpha=0.05):
# Set degrees of freedom
df = len(x) - 1
# Calculate Standard Error
std_error = np.std(x)/np.sqrt(df)
t_statistic = (x.mean() - population_mean)/std_error
# Find critical value
critical_value = t.ppf(1.0 - alpha, df)
# Calculate two-sided p-value
p_value = (1 - t.cdf(abs(t_statistic), df)) * 2
return x.mean(), std_error, t_statistic, critical_value, p_value
# Population mean: 100
t1 = my_ttest_1sample(sample1, 100)
t2 = my_ttest_1sample(sample2, 100)
t3 = my_ttest_1sample(sample3, 100)
t4 = my_ttest_1sample(sample4, 100)
t5 = my_ttest_1sample(sample5, 100)
# Visualization
df = pd.DataFrame([t1, t2, t3, t4, t5],
columns=['sample_mean', 'std_err', 't-statistic', 'critical-value', 'p-value'])
df['less_than'] = df.apply(lambda c: (c['p-value']/2 < 0.05) & (c['t-statistic'] < 0), axis=1)
df['more_than'] = df.apply(lambda c: (c['p-value']/2 < 0.05) & (c['t-statistic'] > 0), axis=1)
df['reject_H0_by_t'] = df.apply(lambda c: abs(c['t-statistic']) > c['critical-value'], axis=1)
df['reject_H0_by_p'] = df.apply(lambda c: c['p-value'] < 0.05, axis=1)
df = df.round(6)
df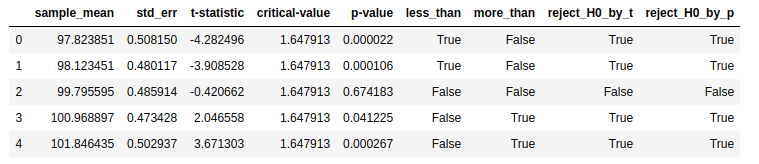
4.2 Two-Sample T-Test (Independent T-Test)
- 독립표본 T 검정
- 독립된 두 그룹간의 평균차이가 있는지 검정
- \[H_0 : u_1 = u_2\]
- \[H_1 : u_1 \ne u_2\]
- 마케팅, A/B테스트시에 두 집단의 평균에 차이가 있는지 검정할때 사용
- Assumptions
- 독립된 두 그룹: 완전히 서로 다른 모수 (populations)을 갖는 다는 뜻이며, 모수가 서로 연결되어 있다면 paired t-test를 한다
- 각 샘플들은 독립적이다. (Independent)
- 정규성을 만족: n > 30 일 경우 만족한다고 판단
- 등분산성을 만족: 두 집단의 분산이 동일하다 (귀무가설을 채택하면, 등분산성을 가정 할 수 있다)
Two-sample T-Test 의 공식은 다음과 같습니다.
\[\begin{align} t &= \frac{\bar{x}_1 - \bar{x}_2}{s_p\sqrt{ \frac{1}{n_1} + \frac{1}{n_2}}} \\ S_p &= \sqrt{\frac{ \sum_{\sim x_1}(x_{i} - \bar{x}_1)^2 + \sum_{\sim x_2}(x_{j} - \bar{x}_2)^2 }{n_1 + n_2 - 2}} = \sqrt{\frac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{(n_1+n_2-2)}} \end{align}\]- \(S_p\): Pooled standard deviation(합동표준편차)
- 합동분산(pooled variance)의 제곱근이다.
- 표본의 크기가 작을때 두 표본을 한데 모아서 한꺼번에 표본표준편차를 계산하게 되는데 이렇게 함면 신뢰도는 높아지지만,
합동표준편차를 사용하기 위해서는 두 모집단의 분산이 동일하다는 가정이 필요하다 - 두 모집단의 분산이 같은지 다른지를 결정하는 것은 F검정을 사용한다
- 쉽게는 \(\frac{1}{2} \le \frac{s_2}{s_1} \le 2\) 가 성립하면 등분산 가정을 성립한다고도 본다
- \(n_1 + n_2 -2\): degrees of freeddom
4.2.1 Scipy
- ttest_ind
- Calculate the T-test for the means of two independent samples of scores.
- This is a two-sided test for the null hypothesis that 2 independent samples have identical average (expected) values.
This test assumes that the populations have identical variances by default. - one-sided p-value는 단순히 two-sided p-value를 반으로 나누면 됨
from scipy.stats import ttest_ind
np.random.seed(2083)
sample1 = np.random.normal(loc=98, scale=10, size=500) # 모수보다 -2
sample2 = np.random.normal(loc=99, scale=10, size=500) # 모수보다 -1
sample3 = np.random.normal(loc=100, scale=10, size=500) # 비교되는 모수
sample4 = np.random.normal(loc=101, scale=10, size=500) # 모수보다 +1
sample5 = np.random.normal(loc=102, scale=10, size=500) # 모수보다 +2
t1 = ttest_ind(sample1, sample3)
t2 = ttest_ind(sample2, sample3)
t3 = ttest_ind(sample3, sample3)
t4 = ttest_ind(sample4, sample3)
t5 = ttest_ind(sample5, sample3)
# Visualization
p_mean, p_std = sample3.mean(), sample3.std(ddof=1)
data = [[p_mean, sample1.mean(), p_std, sample1.std(ddof=1), t1.statistic, t1.pvalue],
[p_mean, sample2.mean(), p_std, sample2.std(ddof=1), t2.statistic, t2.pvalue],
[p_mean, sample3.mean(), p_std, sample3.std(ddof=1), t3.statistic, t3.pvalue],
[p_mean, sample4.mean(), p_std, sample4.std(ddof=1), t4.statistic, t4.pvalue],
[p_mean, sample5.mean(), p_std, sample5.std(ddof=1), t5.statistic, t5.pvalue]]
data = pd.DataFrame(data, columns=['b_mean', 'a_mean', 'b_std', 'a_std', 't-statistic', 'p-value'])
data['less_than'] = data.apply(lambda c: (c['p-value']/2 < 0.05) & (c['t-statistic'] < 0), axis=1)
data['more_than'] = data.apply(lambda c: (c['p-value']/2 < 0.05) & (c['t-statistic'] > 0), axis=1)
data['reject_H0'] = data.apply(lambda c: (c['p-value'] < 0.05) , axis=1)
data = data.round(6)
data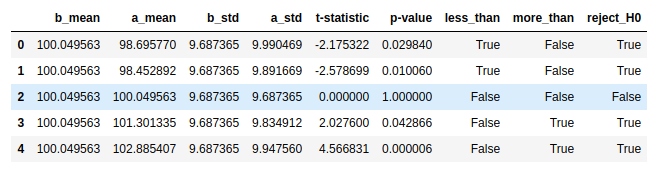
4.2.2 Statsmodels
statsmodels을 사용하면 명시적으로 smaller, larger등으로 단측 검정을 할 수 있으며,
pooled 또는 unequal 등의 옵션으로 Welsh ttest with Satterthwait degrees of freedom 을 사용할수 있다
from statsmodels.stats.weightstats import ttest_ind
statistic1, pvalue1, _ = ttest_ind(sample1, sample3, alternative='two-sided')
statistic2, pvalue2, _ = ttest_ind(sample2, sample3, alternative='two-sided')
statistic3, pvalue3, _ = ttest_ind(sample3, sample3, alternative='two-sided')
statistic4, pvalue4, _ = ttest_ind(sample4, sample3, alternative='two-sided')
statistic5, pvalue5, _ = ttest_ind(sample5, sample3, alternative='two-sided')
s1 = ttest_ind(sample1, sample3, alternative='smaller')
s2 = ttest_ind(sample2, sample3, alternative='smaller')
s3 = ttest_ind(sample3, sample3, alternative='smaller')
s4 = ttest_ind(sample4, sample3, alternative='smaller')
s5 = ttest_ind(sample5, sample3, alternative='smaller')
l1 = ttest_ind(sample1, sample3, alternative='larger')
l2 = ttest_ind(sample2, sample3, alternative='larger')
l3 = ttest_ind(sample3, sample3, alternative='larger')
l4 = ttest_ind(sample4, sample3, alternative='larger')
l5 = ttest_ind(sample5, sample3, alternative='larger')
# T-statistic 의 값은 모두 동일하다
assert (s1[0] == statistic1) and(l1[0] == statistic1)
assert (s2[0] == statistic2) and(l2[0] == statistic2)
assert (s3[0] == statistic3) and(l3[0] == statistic3)
assert (s4[0] == statistic4) and(l4[0] == statistic4)
assert (s5[0] == statistic5) and(l5[0] == statistic5)
# Visualization
data = [[100, sample1.mean(), sample1.std(), statistic1, pvalue1, s1[1], l1[1]],
[100, sample2.mean(), sample2.std(), statistic2, pvalue2, s2[1], l2[1]],
[100, sample3.mean(), sample3.std(), statistic3, pvalue3, s3[1], l3[1]],
[100, sample4.mean(), sample4.std(), statistic4, pvalue4, s4[1], l4[1]],
[100, sample5.mean(), sample5.std(), statistic5, pvalue5, s5[1], l5[1]]]
data = pd.DataFrame(data, columns=['p_mean', 's_mean', 's_std', 't-statistic', 'p-value',
'smaller_p', 'larger_p'])
data['less_than'] = data.apply(lambda c: c['smaller_p'] < 0.05, axis=1)
data['more_than'] = data.apply(lambda c: c['larger_p'] < 0.05, axis=1)
data['reject_H0'] = data.apply(lambda c: (c['p-value'] < 0.05) , axis=1)
data = data.round(6)
data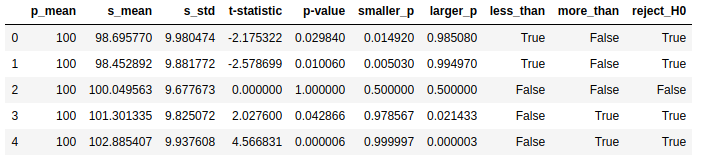
4.2.3 직접 만들어서 사용
from scipy.stats import t
def my_t_test_ind(a, b, alpha=0.05):
n1, n2 = len(a), len(b)
mean1, mean2 = np.mean(a), np.mean(b)
var1, var2 = np.var(a, ddof=1), np.var(b, ddof=1) # ddof=1 매우 중요하다
df1 = n1 - 1
pooled_std = np.sqrt(((n1-1) * var1 + (n2-1) * var2) / (n1 + n2 - 2))
t_statistic = (mean1 - mean2) / (pooled_std * np.sqrt(1/n1 + 1/n2))
# Calculate Critical Value
critical_value = t.ppf(1.0 - alpha, df1)
# Calculate two-sided P-Value
# t.cdf(0) = 0.5 이며, 서로 동일할 경우 t_statistic은 0이 된다.
# symmetric distribution이라는 가정하에서 (당연히 정규분포니까 맞지)
p_value = (1 - t.cdf(abs(t_statistic), n1+n2-2)) * 2
return mean1, mean2, var1, var2, t_statistic, critical_value, p_value
t1 = my_t_test_ind(sample1, sample3)
t2 = my_t_test_ind(sample2, sample3)
t3 = my_t_test_ind(sample3, sample3)
t4 = my_t_test_ind(sample4, sample3)
t5 = my_t_test_ind(sample5, sample3)
# Visualization
df = pd.DataFrame([t1, t2, t3, t4, t5],
columns=['mean_a', 'mean_b', 'var_a', 'var_b',
't-statistic', 'critical-value', 'p-value'])
df['less_than'] = df.apply(lambda c: (c['p-value']/2 < 0.05) & (c['t-statistic'] < 0), axis=1)
df['more_than'] = df.apply(lambda c: (c['p-value']/2 < 0.05) & (c['t-statistic'] > 0), axis=1)
df['reject_H0_by_t'] = df.apply(lambda c: abs(c['t-statistic']) > c['critical-value'], axis=1)
df['reject_H0_by_p'] = df.apply(lambda c: c['p-value'] <= 0.05, axis=1)
df = df.round(6)
df
4.3 Paired T-Test (Dependent Sample T-Test)
- 대응표본 T 검정
- 독립표본 T 검정은 서로 다른 집단간의 평균에 유의미한 차이가 있는지를 알아보는 것이고,
대응표본 T 검정은 동일한 집단에 대해서 사전 그리고 사후 등의 차이를 보고자 할때 사용
예를들어, 특정 약물이 동일한 환자집단에게 사용시 사용전 그리고 사용후의 혈당수치에 유의미한 차이가 있는지를 보고자 할때 사용 - \[H_0 : u_1 = u_2\]
- \[H_1 : u_1 \ne u_2\]
- Assumptions
- 종속변수 (dependent variable)은 반드시 continuous (intervla/ratio) 변수이어야 한다
- 관측값은 서로 독립성을 갖어야 한다
- 종속변수은 정규분포를 따라야 한다
- 종속변수는 outlier를 포함해서는 안된다
Paired T-Test의 공식은 다음과 같습니다.
\[\begin{align} T &= \frac{\bar{d}}{\frac{s_d}{\sqrt{n}}} \end{align}\]- \(\bar{d} = \frac{1}{n} \sum a_i - b_i\) : 두 그룹의 관측치의 차이를 구한다면 여기에 대한 평균값을 구함
- \(s_d\) : 두 그룹의 관측이 차이의 표준편차
4.3.1 Scipy
- ttest_rel
- Calculate the T-test on TWO RELATED samples of scores, a and b
- This is a two-sided test for the null hypothesis that 2 related or repeated samples have identical average (expected) values
from scipy.stats import ttest_rel
np.random.seed(2083)
sample1 = np.random.normal(loc=98, scale=10, size=500) # 모수보다 -2
sample2 = np.random.normal(loc=99, scale=10, size=500) # 모수보다 -1
sample3 = np.random.normal(loc=100, scale=10, size=500) # 비교되는 모수
sample4 = np.random.normal(loc=101, scale=10, size=500) # 모수보다 +1
sample5 = np.random.normal(loc=102, scale=10, size=500) # 모수보다 +2
t1 = ttest_rel(sample1, sample3)
t2 = ttest_rel(sample2, sample3)
t3 = ttest_rel(sample3, sample3)
t4 = ttest_rel(sample4, sample3)
t5 = ttest_rel(sample5, sample3)
# Visualization
p_mean, p_std = sample3.mean(), sample3.std(ddof=1)
data = [[p_mean, sample1.mean(), p_std, sample1.std(ddof=1), t1.statistic, t1.pvalue],
[p_mean, sample2.mean(), p_std, sample2.std(ddof=1), t2.statistic, t2.pvalue],
[p_mean, sample3.mean(), p_std, sample3.std(ddof=1), t3.statistic, t3.pvalue],
[p_mean, sample4.mean(), p_std, sample4.std(ddof=1), t4.statistic, t4.pvalue],
[p_mean, sample5.mean(), p_std, sample5.std(ddof=1), t5.statistic, t5.pvalue]]
data = pd.DataFrame(data, columns=['b_mean', 'a_mean', 'b_std', 'a_std', 't-statistic', 'p-value'])
data['less_than'] = data.apply(lambda c: (c['p-value']/2 < 0.05) & (c['t-statistic'] < 0), axis=1)
data['more_than'] = data.apply(lambda c: (c['p-value']/2 < 0.05) & (c['t-statistic'] > 0), axis=1)
data['reject_H0'] = data.apply(lambda c: (c['p-value']/2 < 0.05) , axis=1)
data = data.round(6)
data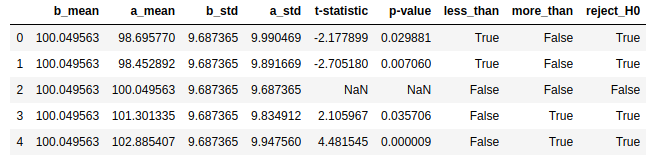
4.3.2 직접 만들어서 사용
def my_ttest_rel(a, b, alpha=0.05):
df = len(a) - 1
d = a - b
d_mean = np.mean(d)
se = np.std(d)/np.sqrt(df)
# T-Statistic
t_statistic = d_mean / se
# Critical Value
critical_value = t.ppf(1.0 - alpha, df)
# Calculate two-sided P-Value
# t.cdf(0) = 0.5 이며, 서로 동일할 경우 t_statistic은 0이 된다.
# symmetric distribution이라는 가정하에서 (당연히 정규분포니까 맞지)
p_value = (1 - t.cdf(abs(t_statistic), df)) * 2
return np.mean(a), np.mean(b), np.var(a), np.var(b), t_statistic , critical_value, p_value
t1 = my_ttest_rel(sample1, sample3)
t2 = my_ttest_rel(sample2, sample3)
t3 = my_ttest_rel(sample3, sample3)
t4 = my_ttest_rel(sample4, sample3)
t5 = my_ttest_rel(sample5, sample3)
# Visualization
df = pd.DataFrame([t1, t2, t3, t4, t5],
columns=['mean_a', 'mean_b', 'var_a', 'var_b',
't-statistic', 'critical-value', 'p-value'])
df['less_than'] = df.apply(lambda c: (c['p-value']/2 < 0.05) & (c['t-statistic'] < 0), axis=1)
df['more_than'] = df.apply(lambda c: (c['p-value']/2 < 0.05) & (c['t-statistic'] > 0), axis=1)
df['reject_H0_by_t'] = df.apply(lambda c: abs(c['t-statistic']) > c['critical-value'], axis=1)
df['reject_H0_by_p'] = df.apply(lambda c: c['p-value'] <= 0.05, axis=1)
df = df.round(6)
df
5. Chi-Square Test
- Pearson Chi-Squared Test 라고도 함
categorical 독립변수와categorical 종속변수사이의 관계를 분석 (따라서 상관관계 분석이라고도 볼 수 있다)- Non-parametric statistic test (비모수통계분석)
- Assumptions
- 종속변수 독립변수모두 nominal (명목) 또는 ordinal (서열) 즉.. categorical data (범주형 데이터)이어야 함
- 만약 비율척도 또는 등간척도의 데이터라면 범주형 데이터로 변형해서 사용 (몸무게 -> 50~60kg / 60~70kg)
- 그룹은 독립성을 갖어야 한다 (남자 vs 여자)
- 기대빈도가 5이하인 데이터가 전체 데이터의 20%를 넘지 않아야 한다
- 표본 크기를 늘린다
- 빈도수가 낮은 그룹을 더 크게 묶는다 (50만원 단위로 묶었다면 -> 100만원 단위로 계층을 나눈다)
- Fisher exact 검정 사용
공식은 다음과 같습니다.
\[\chi^2 = \sum \frac{(O - E)^2}{E}\]- \(O\): the observed value (contingency table로 만들어진 실제 값)
- \(E\): Expected Value (Expected frequency. 아래 pandas로 구현하는 부분 참고)
5.1 Contingency Table (Two-way Frequency Table)
여러개의 categorical variables의 관계를 요약해서 보여줄때 사용하며,
두 변수가 동시에 보이는 일종의 frequency distribution table입니다.
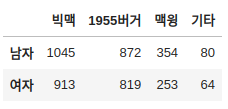
예를 들어서 아래의 테이블은 성인 3000명의 맥도날드 구입을 두개의 그룹으로 분류한것을 보여줍니다.
| 성별 | 빅맥 | 1955버거 | 맥윙 | 기타 | 합계 |
|---|---|---|---|---|---|
| 남자 | 1045 | 872 | 354 | 80 | 2351 |
| 여자 | 913 | 819 | 253 | 64 | 2049 |
| 합계 | 1958 | 1691 | 607 | 144 | 4400 |
Contingency Table의 장점은 여러개가 있습니다.
5.1.1 통계치
아래, 우측의 “합계” 같은 통계치는 확률 계산을 하는데 유용하게 사용될 수 있습니다.
- ex) 빅맥을 고를 확률: \(\frac{1958}{4400} = 0.445\)
5.1.2 Conditional probability
Conditional probability 계산하는데 유용하게 사용할 수 있습니다.
- 남자라는 조건을 가정하에, 1955버거를 좋아할 확률: \(\frac{872}{2351} = 0.37\)
- 1955를 좋아한다는 가정하에, 남자일 확률: \(\frac{872}{1691} = 0.5156\)
5.1.3 Expected frequency
Expected frequency 를 계산할때도 편하게 사용할 수 있습니다.
\[E_{cr} = \frac{r \cdot c}{n}\]- r: sum of row
- c: sum of column
- n: sample size
예를 들어서, 맥윙을 선호하는 남자들의 기대값 (expected number)는 대략 다음과 같습니다.
\[\mathbb{E}_{남자, 맥윙} = \frac{2351 * 607}{4400} \approx 324.33\]324.33이라는 값은 354라는 값보다 작으며, 기대값보다 더 작은 값이라는 것을 알 수 있습니다. (less than expected)
여자쪽을 구하는 것은 다시 계산 할수도 있지만 맥윙을 좋아하는 사람 - 맥윙을 좋아하는 남자 기대값 을 해도 됩니다 (그 반대가 여자이기 때문에)
expected frequency를 알면 좋은 점은 two variables의 독립성을 검정할 수 있습니다.
즉 예제의 경우, Gender(남자, 여자), 좋아하는 메뉴 가 독립적인지 아닌지를 검정할 수 있습니다.
방법은 모든 cell의 expected frequency를 계산한 다음, observed frequency와 비교를 한 후, chi-squared test를 하면 됩니다.
5.2 Chi Square Test in Pandas
- 두 categorical variables 이 서로 독립적인지 (연관성이 없음) 또는 종속적인지 (연관성이 있음) 검정 할 수 있습니다.
- 오직 categorical data (성별, 색상) 에만 사용될 수 있습니다.
- 모든 셀 (each entry)는 최소한 모두 5를 넘어야 합니다. (위의 예제에서 가장 작은 값은 80으로서 chi square test 가능)
예제로 주어진 데이터에 대한 chi square test 계산 방법은 다음과 같습니다.
먼저 Pandas dataframe으로 만듭니다.
columns = ['빅맥', '1955버거', '맥윙', '기타']
index = ['남자', '여자']
data = [[1045, 872, 354, 80],
[913, 819, 253, 64]]
df = pd.DataFrame(data, columns=columns, index=index)
df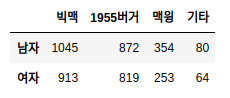
각각의 셀마다 expected frequency를 계산합니다.
total_n = df.values.sum()
gender_sums = df.sum(axis=1).values
product_sums = df.sum(axis=0).values
expected_frequencies = np.round(product_sums * gender_sums.reshape(-1, 1) / total_n, 2)
print('total_n :', total_n)
print('gender_sums :', gender_sums)
print('product_sums:', product_sums)
print('\nExpected Frequency')
ev = pd.DataFrame(expected_frequencies, columns=columns, index=index)
ev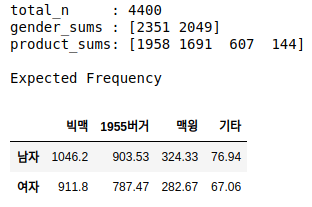
샘플 데이터의 실제 관측치 값에서 expected frequency를 subtract한후 -> 제곱 -> 다시 expected frequency로 나눠줍니다.
이후 모두 합하면 chi-square 값이 나옵니다.
chi_square_df = (df - ev)**2/ev
chi_square_value = chi_square_df.values.sum()
display(chi_square_df)
print('chi square statistic:', chi_square_value)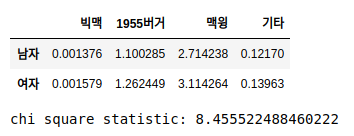
P-value를 찾기 위해서는 먼저 degrees of freedom을 계산해주어야 합니다.
\[\begin{align} DF &= (n\_rows -1) * (n\_columns -1) \\ &= (2-1) * (4-1) \\ &= 3 \end{align}\]1 - cdf(chi_square_statistic, df=degree of freedom) 을 사용해서 p-value를 알아낼수 있습니다.
예제의 경우 p-value값은 0.037로서 0.05보다 작음으로 (0.037 < 0.05),
성별과 좋아하는 상품에는 서로 종속적(연관성이 있다)이라고 말할수 있습니다.
from scipy.stats import chi2
p_value = 1 - chi2.cdf(abs(chi_square_value), df=3)
print('p-value:', p_value)p-value: 0.037478319029283225Critical value로 검정은 ppf(0.95, df=degree of freedom) 을 사용합니다.
- if abs(statistic) <= critical value: 귀무가설을 채택하며, 두 변수는 서로 독립적이다 (서로 영향이 없다)
- if abs(statistic) > critical value: 귀무가설을 기각하며, 두 변수는 서로 종속적이다. (서로 영향이 있다)
critical_value = chi2.ppf(0.95, df=3)
print('critical value :', critical_value)
print('chi square statistic:', chi_square_value)
if critical_value < abs(chi_square_value):
print('귀무가설 기각 - Dependent > 서로 영향이 있다')
else:
print('귀무가설 채택 - Independent > 서로 영향이 없다')critical value : 7.814727903251179
chi square statistic: 8.455522488460222
귀무가설 기각 - Dependent > 서로 영향이 있다5.3 Chi Square Test in Scipy
Scipy를 사용하면 매우 쉽게 해결할 수 있습니다.
먼저 빈도테이블 (contingency table) 을 생성해야 합니다.
예제에서는 테이블을 직접 만들었지만, 실무에서는 pd.crosstab 을 사용해서 만들면 편합니다.
columns = ['빅맥', '1955버거', '맥윙', '기타']
index = ['남자', '여자']
data = [[1045, 872, 354, 80],
[913, 819, 253, 64]]
df = pd.DataFrame(data, columns=columns, index=index)
df
chi2_contingency 함수를 사용하고, contingency table을 넣으면 끝입니다.
(이때 테스트 하고자 하는 그룹만 넣으면 됩니다. 예제에서는 남자, 여자 2개지만, 여러개의 AB Test Groups 이 존재시, 2개씩 넣어서 테스트 합니다.)
from scipy.stats import chi2_contingency
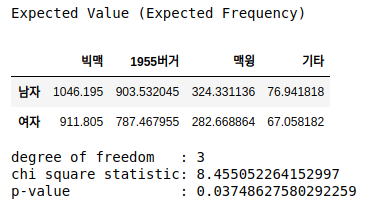
chi_statistic, p_value, dof, expected_df = chi2_contingency(df)
print('Expected Value (Expected Frequency)')
display(pd.DataFrame(expected_df, columns=columns, index=index))
print('degree of freedom :', dof)
print('chi square statistic:', chi_statistic)
print('p-value :', p_value)