Performance Test For Multi Class Classification
Easy Way
Classification Report
from sklearn.metrics import classification_report
y_true = [0, 0, 1, 1, 1, 1, 1, 2, 2, 3]
y_pred = [0, 2, 1, 1, 2, 0, 0, 2, 2, 0]
print(classification_report(y_true, y_pred)) precision recall f1-score support
0 0.25 0.50 0.33 2
1 1.00 0.40 0.57 5
2 0.50 1.00 0.67 2
3 0.00 0.00 0.00 1
accuracy 0.50 10
macro avg 0.44 0.47 0.39 10
weighted avg 0.65 0.50 0.49 10Confusion Matrix
- Row: True Label
- Column: Predicted Label
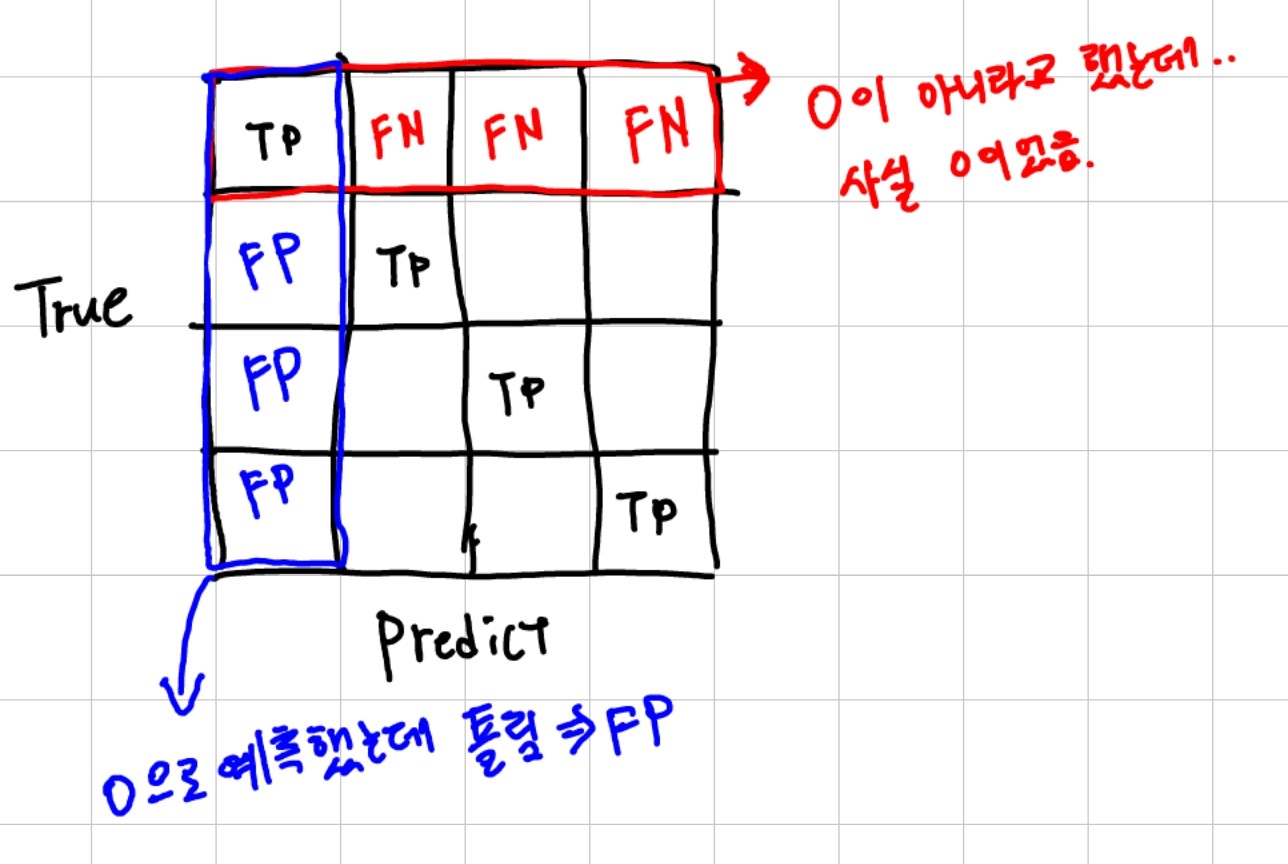
- TP 예제: [0, 0, 1, 1, 2, 2] GT에서 [0, 0, 1, 1, 2, 2] 예측시, 다 맞음.
- FP 예제: [0, 0, 1, 1, 2, 2] GT에서 [0, 0, 0, 0, 0, 0] 예측시, 0의 FP는 1번을 0으로 예측하고, 2를 0으로 예측한 것을 FP로 봄 (0을 0으로 예측한건 TP)
- FN 예제: [0, 0, 1, 1, 2, 2] GT에서 [2, 2, 0, 0, 1, 1] 예측시, 각 레이블마다 고양이는 강아지라고, 자동차는 사람이라고 예측했는데 다 틀림.
from sklearn.metrics import confusion_matrix
import seaborn as sns
y_true = [0, 0, 1, 1, 1, 1, 1, 2, 2, 3]
y_pred = [0, 2, 1, 1, 2, 0, 0, 2, 2, 0]
cm = confusion_matrix(y_true, y_pred)
print(cm)
sns.heatmap(cm, cmap='YlGnBu')[[1 0 1 0]
[2 2 1 0]
[0 0 2 0]
[1 0 0 0]]

Performance Test
Accuracy
\[\text{Accuracy} = \frac{TP + TN}{N}\]from sklearn.metrics import accuracy_score
y_true = [0, 0, 1, 1, 1, 1, 1, 2, 2, 3]
y_pred = [0, 2, 1, 1, 2, 0, 0, 2, 2, 0]
acc = accuracy_score(y_true, y_pred)
acc_norm = accuracy_score(y_true, y_pred, normalize=False)
print('n:', len(y_true))
print(f'Accuracy : {acc:.2}')
print(f'Normalized Accuracy: {acc_norm}')n: 10
Accuracy : 0.5
Normalized Accuracy: 5Accuracy from Confusion Matrix
def cal_accuracy(cm):
"""
대각선으로 (TP + TN) 모두 합하고, 전체 N 값으로 나눈다
"""
return np.diagonal(cm).sum() / cm.sum()
cm = confusion_matrix(y_true, y_pred)
print('Accuracy:', cal_accuracy(cm))Accuracy: 0.5Recall (Sensitivity, True Positive Rate)
\[\text{True Positive Rate} = \frac{TP}{TP + FN}\]- 단점: 전부다 1로 예측하면, TP는 다 맞추고, FN은 0이 되면서, recall의 예측값은 1이 된다
average parameter
- None : 각각의 클래스마다의 recall값을 계산한다
- binary: (default) binary classification에서 사용
- micro : 전체 클래스 데이터 관점에서의 total true positives, false negatives, false positives 를 계산
- macro : 각각의 label마다의 recall의 unweighted mean을 계산한다. 따라서 label imbalance를 고려하지 않는다
from sklearn.metrics import recall_score
y_true = [0, 0, 1, 1, 1, 1, 1, 2, 2, 3]
y_pred = [0, 2, 1, 1, 2, 0, 0, 2, 2, 0]
recalls = recall_score(y_true, y_pred, average=None)
recall_micro = recall_score(y_true, y_pred, average='micro')
recall_macro = recall_score(y_true, y_pred, average='macro')
recall_weighted = recall_score(y_true, y_pred, average='weighted')
print('Recalls :', recalls)
print(f'Recall (micro) : {recall_micro:.2}')
print(f'Recall (macro) : {recall_macro:.2}')
print(f'Recall (weighted): {recall_weighted:.2}')Recalls : [0.5 0.4 1. 0. ]
Recall (micro) : 0.5
Recall (macro) : 0.47
Recall (weighted): 0.5Recall From Confusion Matrix
def cal_recall(cm, average=None):
data = [np.nan_to_num(cm[i, i] / cm[i, :].sum()) for i in range(cm.shape[0])]
data = np.array(data)
if average is None:
return data
elif average == 'macro':
return data.mean()
elif average == 'micro':
weight = cm.sum(axis=1)
return (data * weight).sum() / weight.sum()
return data
cm = confusion_matrix(y_true, y_pred)
print('recalls :', cal_recall(cm, average=None))
print('recalls (macro):', cal_recall(cm, average='macro'))
print('recalls (micro):', cal_recall(cm, average='micro'))recalls : [0.5 0.4 1. 0. ]
recalls (macro): 0.475
recalls (micro): 0.5Precision
\[\text{Precision} = \frac{TP}{TP + FP} = \frac{TP}{\text{Predicted Yes}}\]- 단점: FP가 없는 경우 100% 맞은 것으로 나옴.
- 아래 1의 경우, 다른 레이블 (0, 2, 3) 에서 어떠한 예측값에서 1이 없습니다. (False Positive가 없음)
- 즉, “고양이” 예측을 단 한번만 맞추고, 다른 모든 예측 값을 “강아지”로 하면 precision은 100% 다 맞춘것으로 나옵니다.
from sklearn.metrics import precision_score
y_true = [0, 0, 1, 1, 1, 1, 1, 2, 2, 3]
y_pred = [0, 2, 1, 1, 2, 0, 0, 2, 2, 0]
precisions = precision_score(y_true, y_pred, average=None)
precision_micro = precision_score(y_true, y_pred, average='micro')
precision_macro = precision_score(y_true, y_pred, average='macro')
precision_weighted = precision_score(y_true, y_pred, average='weighted')
print('Precisions :', precisions)
print(f'Precision (micro) : {precision_micro:.2}')
print(f'Precision (macro) : {precision_macro:.2}')
print(f'Precision (weighted): {precision_weighted:.2}')Precisions : [0.25 1. 0.5 0. ]
Precision (micro) : 0.5
Precision (macro) : 0.44
Precision (weighted): 0.65Precision from Confusion Matrix
def cal_precision(cm, average=None):
data = [np.nan_to_num(cm[i, i] / cm[:, i].sum()) for i in range(cm.shape[0])]
data = np.array(data)
if average is None:
return data
elif average == 'macro':
return data.mean()
elif average == 'micro':
weight = cm.sum(axis=0)
return (data * weight).sum() / weight.sum()
return data
print(f'Precisions : {cal_precision(cm)}')
print(f'Precision (macro) : {cal_precision(cm, average="macro"):.2}')
print(f'Precision (micro) : {cal_precision(cm, average="micro"):.2}')Precisions : [0.25 1. 0.5 0. ]
Precision (macro) : 0.44
Precision (micro) : 0.5F1 Score
\[\text{F1 Score} = 2 \cdot \frac{\text{precision} \times \text{recall}}{\text{precision} + \text{recall}}\]from sklearn.metrics import f1_score
y_true = [0, 0, 1, 1, 1, 1, 1, 2, 2, 3]
y_pred = [0, 2, 1, 1, 2, 0, 0, 2, 2, 0]
f1_score(y_true, y_pred, average=None)
f1 = f1_score(y_true, y_pred, average=None)
f1_micro = f1_score(y_true, y_pred, average='micro')
f1_macro = f1_score(y_true, y_pred, average='macro')
f1_weighted = f1_score(y_true, y_pred, average='weighted')
print('F1 :', f1)
print(f'F1 (micro) : {f1_micro:.2}')
print(f'F1 (macro) : {f1_macro:.2}')
print(f'F1 (weighted): {f1_weighted:.2}')F1 : [0.33333333 0.57142857 0.66666667 0. ]
F1 (micro) : 0.5
F1 (macro) : 0.39
F1 (weighted): 0.49