정말 오랜만에 블로그글을 작성하네요.. ㅎㄷㄷㄷㄷ
근래에 Faster R-CNN 그리고 RetinaNet 까지 논문읽고 구현하느라.. 무척바빴습니다.
처음 시작은.. 좀 쉬운내용 공유하고자 합니다.

Confusion Matrix

Confusion Matrix는 일반적으로 classification model이 테스트 데이터에 대한 performance를 측정하는데 사용됩니다. (ground-truth values를 알고 있는 상태) confusion matrix는 상대적으로 꽤 쉽게 이해할수 있기 때문에 많이 사용됩니다. 다만 용어가 매우 혼돈스럽기 때문에 주의가 필요합니다.

Binary Classification

아래의 matrix는 165명의 환자를 대상으로 질병이 있는지 없는지 예측한 값과, 실제 값을 나타낸 것 입니다.

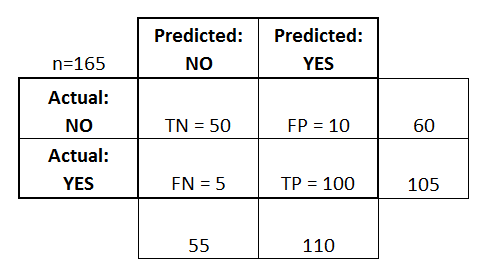
Confusion Matrix

  • True Positives (TP): 질병이 있다고 예측했고 실제로 질병이 있는 경우 (있는게 맞어)
  • True Negatives (TN): 질병이 없다고 예측했고, 실제로 질병이 없는 경우 (없는게 맞어)
  • False Positives (FP): 질병이 있다고 예측했지만, 실제로는 질병이 없음 (있는게 틀려)
  • False Negatives (FN): 질병이 없다고 예측했지만, 실제로는 질병이 있음 (없는게 틀려)

Positives, Negatives는 예측한 값을 의미하고, True, False는 그 예측한 값이 맞냐 틀리냐를 말하는 상대적 개념

Performance Measures

일반적으로 classification에서 accuracy를 많이 보지만, 실무에서는 이것만 보지는 않습니다.
아래와 같은 analysis들을 보면서 해석을 합니다.

자세한 내용은 위키피디아 Confusion Matrix를 참고 합니다.

Accuracy

  • 전체 샘플중에 실제로 맞춘 비율
  • 가장 많이 사용되지만, class간의 비율이 동일할때 사용합니다.
  • 최적화에서 objective function으로 사용됩니다.
\[\text{Accuracy} = \frac{TP + TN}{N} = \frac{100 + 50}{165} = 0.91\]

Error Rate (Misclassification Rate)

  • 1 - accuracy
  • 얼마나 못 맞췄냐?
\[\text{Misclassification Rate} = \frac{FP + FN}{N} = \frac{10 + 5}{165} = 0.09\]

Recall (Sensitivity, True Positive Rate)

  • 실제 암에 걸린 환자들중 제대로 암이라고 판단한 비율
  • 실제 사기범들중에 유죄 판정을 내린 비율
  • 사기친 거래들중에 실제로 잡아낸 비율 -> 검거율!
  • 값이 높을수록 좋다
\[\text{True Positive Rate} = \frac{TP}{TP + FN} = \frac{TP}{\text{Actual Yes}} = \frac{100}{100 + 5} = 0.95\]

Fall-out (False Alarm Ratio, False Positive Rate)

  • 실제로는 암이 아닌데 암이라고 말하는 비율
  • 실제로는 유죄가 아닌데 유죄라고 판결하는 비율
  • 실제로는 임신이 아닌데 임신이라고 오작동 하는 비율
  • 실제 정상거래들중, 사기라고 예측한 비율
  • 오판율
  • 1 - Specificity
  • 값이 높을수록 병신갖은 예측/판단을 한거다
\[\text{True Positive Rate} = \frac{FP}{FP + TN} = \frac{FP}{\text{Actual No}} = \frac{10}{10 + 50} = 0.17\]

Specificity

  • 실제 아닌데, 예측도 아니라고 한 비율
  • 실제 암이 없는 정상인 중에, 예측도 암이 없다고 판단한 비율
  • 실제 무죄인 사람들 중에, 예측도 무죄라고 판단한 비율
  • 값이 높을수록 좋다
  • 1 - False Positive Rate
\[\text{Specificity} = \frac{TN}{TN + FP} = \frac{TN}{\text{Actual No}} = \frac{50}{50 + 10} = 0.83\]

Precision

  • 질병이 있다고 예측한 것중에 실제로 맞춘 비율 -> 값이 낮을 수록 암에 걸렸다고 진단했는데.. 실제로는 아닌 사람들이 있다.
  • 사기 거래에서 실제 사기를 제대로 잡아낸 비율 -> 값이 낮을 수록 무죄인 사람이 유죄로 잡혀 들어간 꼴이다.
\[\text{Precision} = \frac{TP}{TP + FP} = \frac{TP}{\text{Predicted Yes}} = \frac{100}{100 + 10} = 0.91\]

F1 Score (F-measure)

F1 Score는 precision과 recall의 조합으로 하나의 수치로 나타냅니다.

예를 들어서 다음과 같은 암을 진단하려는 사람들이 있습니다.

\[\text{실제 암환자} = \{ A, B, C \}\] \[\text{실제 정상인} = \{ D, E, F \}\]

Precision의 문제점

Precision의 문제는 만약 예측한 값들중 (pred_y) 그중 맞은 갯수이기 때문에..
만약 A 한명만 암이 있다고 진단하고 나머지는 정산으로 예측한다면 precision은 1값으로 나옵니다.

\[\text{Precision} = \frac{TP}{TP + FP} = \frac{1}{1 + 0} = 1\]

FN에 B, C 가 존재하지만, Precision은 FN을 사용하지 않기 때문에 이렇게 나옵니다.

Recall의 문제점

만약 모든 사람 A, B, C, D, E, F 를 모두 암환자로 예측했다면.. Recall의 공식은 다음과 같아집니다.

\[\text{Recall} = \frac{TP}{TP + FN} = \frac{3}{3 + 0} = 1\]

분명히 정상인 환자를 암이 있는 환자로 분류했는데도 불구하고 수치는 매우 높게 나옵니다.

FP 에 D, E, F가 존재하지만 Recall은 FP를 사용하지 않죠.

Precision + Recall = F1 Score

따라서 Precision과 Recall을 서로 조합하여 단점을 보완하고 하나의 수치로 만든것이 F1 Score입니다.
Harmonic Mean을 사용한 F1 Score의 공식은 다음과 같습니다.

\[\text{F1 Score} = 2 \cdot \frac{\text{precision} \times \text{recall}}{\text{precision} + \text{recall}}\]

여기서 Harmonic Meam (조화 평균)은 일반적으로 사용하는 arithmetic mean (산술 평균)과는 의미가 다릅니다.
Harmonic mean은 reciprocal을 사용합니다.

\[\begin{align} \text{Arithmetic Mean} &= \frac{1}{n} \sum^n_{i=1} x_i = \frac{x_1 + x_2 + ... + x_n}{n} \\ \text{Harmonic Mean} &= \left( \frac{1}{n} \sum^n_{i=1} x_i^{-1} \right)^{-1} = \frac{n}{\frac{1}{x_1} + \frac{1}{x_2} + ... + \frac{1}{x_n}} \end{align}\]

F1 score는 harmonic mean을 사용하는데 이때 elements가 precision 그리고 recall 2개 이기 때문에 공식은 다음과 같습니다.
x1 = precision, x2 = recall, n=2 로 가정

\[\text{F1 Score} = \frac{2}{\frac{1}{x_1} + \frac{1}{x_2}} = 2 \cdot \frac{x_1 \times x_2}{x_1 + x_2} = 2 \cdot \frac{\text{precision} \times \text{recall}}{\text{precision} + \text{recall}}\]

ROC (Receiver Operating Characteristics)

이름이 참 이상합니다. Receiver Operating Characteristics 라니.. (직역하면.. 수신기 작동 특성?)
2차 대전때, 진주만 습격 이후로, 미군은 일본 비행기를 감지하는 레이더 시그널에 대해서 연구를 하기 시작합니다.
레이더 수신기 장비 (Radar receiver operators)의 성능을 측정하기 위해서 사용한 방법은 Receiver Operating Characteristics 입니다.
결론적으로 일본 전투기를 제대로 감지하는지 레이더의 성능을 측정하기 위한 방법으로 생겨났고.. 그래서 이름도 이렇게 됨.

ROC curve 그래프는 세로축을 True Positive Rate (Sensitivity or Recall) 로 하고, 가로축을 False Positive Rate 으로 시각화한 그래프로서 각각의 classification thresholds마다 TPR VS FPR 을 계산한 그래프입니다. 중간의 직선은 reference line 입니다.

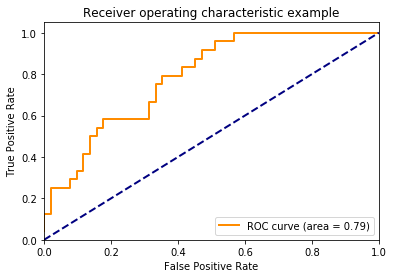
ROC Curve

  • TPR이 높고, FPR은 낮을수록 좋은거 입니다.

TPR과 FPR은 서로 반비례적인 관계에 있습니다.

AUC (Area Under the ROC Curve)

ROC curve의 밑면적을 계산한 값입니다.

AUC