Importance Sampling

Introduction to Importance Sampling

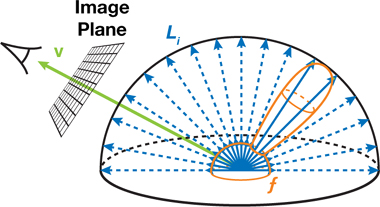
아래의 토끼는 배경에서 반사된 빛을 받아서 다시 재반사(reflect)하여 카메라에 투영된 이미지의 모습입니다.

3D rendering으로 나온 토끼의 이미지처럼, 특정 방향 \(L_i(\mathbf{u})\) 으로부터 들어오는 빛을 받아서, 카메라 \(\mathbf{v}\) 방향으로 재반사 하기 위해서는, Bidirectional reflectance distribution function (BRDF) 라는 material function \(f\) 를 사용합니다. 전체 반사되는 빛 \(L_0(\mathbf{v})\) 의 양을 계산하기 위해서는 모든 각각의 방향 \(\mathbf{u}\) 으로부터 오는 모든 빛을 합 하거나 또는 integration해야 합니다. 공식은 다음과 같습니다.

\[L_0(\mathbf{v}) = \int_H L_i(\mathbf{u}) f(\mathbf{u}, \mathbf{v}) \cos \theta_u \ du\]

공식을 자세하게 알 필요는 없습니다.
포인트는 모든 방향에서는 오는 빛을 계산하여 반사되는 빛을 계산하여 적분하는것은 계산의 양이 너무나 많기 때문에 할 수 없는 방법입니다.
따라서 uniform distribution으로 랜덤으로 들어오는 빛을 samples로 integral을 계산합니다. 샘플들의 평균은 해당 integral의 approximation과도 같습니다.

만약 integrated function이 어떻게 작동하는줄 대략적으로 알고 있다면,
Uniform ramdom directions로부터 integral을 approximation하는 것은 좋은 방법이 아닙니다.
예를 들어서 카메라에 반사되는 빛을 구하기 위해서, 사물에 닿는 모든 빛을 구하는게 아니라, 바로 거울 처럼 반사되는 지점에서 오는 빛을 samples로 사용하는 것이 좋을 것입니다. 왜냐하면 대부분의 카메라에 반사되는 빛은 해당 방향으로부터 빛이 오기 때문입니다.

수학적으로 표현하기 위해서, probability density function (PDF)를 사용하여 샘플링을 위한 최적의 방향을 정하게 됩니다.
PDF는 normalized function이며, PDF함수의 전체 도메인에 대한 integral의 값은 1이고, 샘플링에 가장 중요한 지점은 peaks로 나타나게 됩니다.

Variance Reduction

Monte Carlo integration의 퀄리티를 높이기 위해서는 variance 를 낮춰야 합니다.
Monte Carlo에서 사용되는 Samples들은 independent하기 때문에 \(\sigma^2 \left[ \sum_i Y_i \right] = \sum_i \sigma^2 [Y_i]\) property를 이용해서 문제를 더 간결하게 만들수 있습니다.

\[\begin{align} \sigma^2\left[ \langle F^N \rangle \right] &= \sigma^2 \left[ \frac{1}{N} \sum^{N-1}_{i=0} \frac{f(X_i)}{pdf(X_i)} \right] &[1] \\ &= \frac{1}{N^2} \sum^{N-1}_{i=0} \sigma^2 \left[ \frac{f(X_i)}{pdf(X_i)} \right] &[2] \\ &= \frac{1}{N^2} \sum^{N-1}_{i=0} \sigma^2 [Y_i] &[3] \\ &= \frac{1}{N} \sigma^2[Y] &[4] \end{align}\]

따라서…

\[\sigma \left[ \langle F^N \rangle \right] = \frac{1}{\sqrt{N}} \sigma[Y]\]
  • \[Y_i = \frac{f(X_i)}{pdf(X_i)}\]
  • \(Y\) : 어떤 특정 \(Y_i\) 의 값을 뜻합니다. 예를 들어서 \(Y = Y_2\) 또는 \(Y = Y_3\)

위의 유도공식(derivation)은 위에서 언급한 standard deviationdms \(O(\sqrt{N})\) 로 converge가 되는 것을 증명합니다.
각각의 \(Y_i\) 의 variance를 낮춤으로서 전체적인 \(\langle F^N \rangle\) 의 variance또한 낮춰줍니다.

Variance Reduction 기법은 각각의 \(Y_i\) 를 가능하면 constant로 만들려고 하는 것입니다. 이를 통해서 전체적인 에러률을 낮춥니다.

왜 f(x) 를 pdf(x) 로 나누려고 하는지 직관적으로 설명하겠습니다.
pdf가 높다는것은 random variable \(X\) 가 어떤 값 \(x_i\) 을 가져올 확률을 높여줍니다.
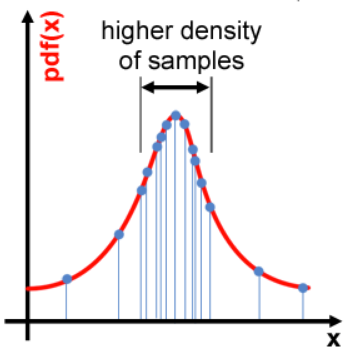
예를 들어 아래 그림의 normal distribution에서 중앙에 samples들이 몰려있기 때문에 중앙부분..즉 높은 pdf값을 갖은 samples들을 Monte Carlo 알고리즘에 사용이 될 것입니다. 즉 위의 예제처럼 면적을 구하고자 할때.. y축으로 높은 부분을 사용해서 계산하기 때문에 당연히 결과값도 bias가 생기게 될 것입니다.

하지만 f(x) 를 pdf(x)로 나누면 확률이 높은 부분은 더 낮아지고, 반대로 확률이 적은 부분은 높아지게 됩니다.
예를 들어서 rare한 부분의 sample의 경우 1/0.1 = 10 처럼 값이 더 올라가게 됩니다.

No Prior Knowledge on the Integrated Function

위에서 저런 가설이 사용가능한 이유는 Integrated function에 대해서 알고 있기 때문입니다.
하지만 대부분의 경우에는 integrated function에 대해서 사전에 지식이 없는 경우가 대부분이며, 어느 부분이 중요한지 알아서 샘플링은 불가능 합니다.

여기서 Variance Reduction과 상충되게 됩니다.
Variance Reduction 은 integrated function에 대해서 사전에 알고 있어야 하지만 현실은 대부분의 경우 모른다는 것입니다.

가장 이상적인 상황은 다음과 같습니다.
Integrand를 non-constant function에서 constant function으로 만들어주면 됩니다.
Constant function으로 만든다는 뜻은 variance은 0으로 만들며 approximation은 항상 동일한 값을 얻는다는 뜻입니다.
이는 Monte Carlo Integration의 목표가 variance를 최대한 작게 만들고, samples은 최대한 적은 양을 사용하는 것과도 부합합니다.
아래의 그림처럼 constant function이 되면 uniform distribution으로 samples을 얻을 수 있게 됩니다.

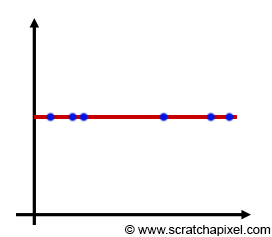
물론 이는 가장 이상적인 상황일때 입니다. 실제로 이런 일은 일어나기 쉽지 않습니다.

Convert Non-Constant Function to Constant Function

함수를 자기자신과 나누어 버리면 항상 결과값은 1이 나오게 됩니다.
예를 들어서 \(f(0)=2\) 일때 \(\frac{f(0)}{2} = 1\) 이 되고,
\(f(2)=0.5\) 일때 \(\frac{f(2)}{0.5} = 1\) 이 되게 됩니다.

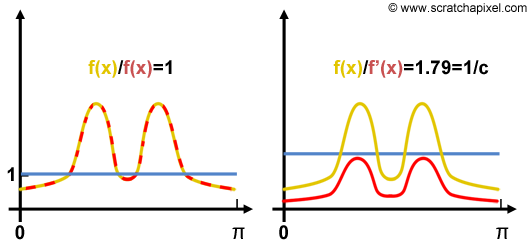
General Monte Carlo integration \(\langle F^N \rangle = \frac{1}{N} \sum^{N-1}_{i=0} \frac{f(x_i)}{pdf(x_i)}\) 에서 \(pdf(x_i)\) 부분을 \(pdf(x_i) = cf(x_i)\) 바꿔서줄 수 있습니다.
(이때 조건은 가장 이상적인 상황으로서 \(pdf(x_i)\) 는 integral과 정확히 또는 매우 유사하게 비례한다고 가정한다.
따라서 2번째 그림처럼 위치는 다르지만 비율은 동일하기 때문에 \(f(x) = cf'(x)\) 가 된다)

\[\require{enclose} Y_i = \frac{f(X_i)}{pdf(X_i)} = \frac{ \enclose{updiagonalstrike}{f(X_i)}}{ c \enclose{updiagonalstrike}{f(X_i)}} = \frac{1}{c}\]

각각의 \(Y_i\) 는 동일한 값을 리턴하기 때문에, 전체적으로 variance도 0입니다.

c를 유도하는 방법은 PDF가 integrate하면 1이 되는 점을 이용합니다.
\(pdf(X_i) = cf(X_i)\) 이므로.. \(\int cf(X_i) = 1\) 이 됩니다.
상수에 대한 곱은 intgration rule에서 밖으로 빠질수 있으므로 \(c \int f(X_i) = 1\) 가 됩니다.
여기서 다시 \(\int f(X_i)\) 를 우측으로 보내면 아래와 같은 공식이 나오게 됩니다.

\[c = \frac{1}{\int f(x)\ dx}\]

해당 공식은 불행하게도 integral \(f(x)\) 를 연산해야지만 pdf에서 사용되는 normalization constant \(c\) 를 얻을수 있다는 것을 보여줍니다.
즉 이 방법을 사용하기 위해서는 \(c\) 를 알아야 하는데.. 애초 처음에 integral \(f(x)\) 를 연산을 처음에 해놔야 한다는 뜻입니다.

따라서 실제 적용은 매우 어려운 경우가 많습니다. (일단 integral f(x)를 한다는 것 자체를 모르기 때문에 못하는 경우가 많기 때문에)
아래 그림에서 파란색은 intgrand function 이고 빨간색은 pdf를 나타냅니다.

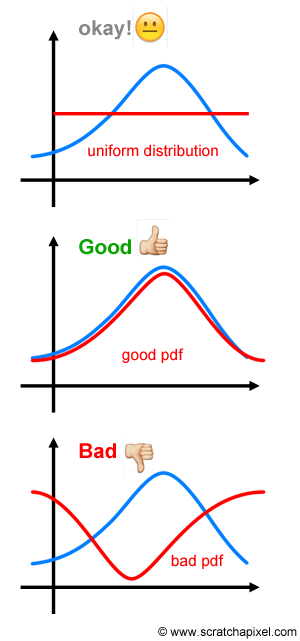
만약 integrand function의 shape에 대해서 전혀 모른다면 그냥 uniform distribution으로 가는게 좋습니다.
물론 pdf와 intgrand가 유사한 분포를 갖고 있는것보다는 좋지 않겠지만.. 잘못 선택하여 전혀 다른 분포를 갖은 pdf 를 사용하는 것 보다는 낫습니다.

Example

다음의 integral를 Monte Carlo Integration을 사용하여 \(sin(x)\) 함수를 approximate합니다.

\[F = \int^{\pi/2}_{0} sin(x)\ dx\]

Second fundamental of calculus에 따르면 antiderivate of \(sin(x)\) 는 \(- cos(x)\) 이므로 다음과 같이 쓸수 있습니다.

\[\begin{align} F &= \left[ - \cos \left( x \right) \right]^{\frac{\pi}{2}}_0 \\ &= - cos\left( \frac{\pi}{2} \right) - (- cos(0)) \\ &= 1 \end{align}\]

해당 integral의 결과값은 1입니다.
해당 integral을 Monte Carlo integration으로 위의 integral을 approximate하겠습니다.
이때 2개의 서로다른 pdf를 사용합니다.

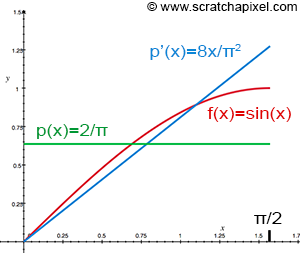
  • 1) \(\text{Uniform probability distribution} (p(x) = \frac{2}{\pi x})\)
  • 2) \(\text{pdf}(p'(x) = \frac{8x}{\pi^2})\)

아래 그림에서 보듯이 두번째 PDF가 uniform probability distribution보다 integrand의 shape에 더 유사합니다.
위에서 배운 이론대로라면 uniform probability distribution보다 두번째 PDF가 variance를 더 줄여줍니다.

첫번째 Uniform Distribution에 대해서..

  • Uniform distribution에는 다음의 estimator를 사용합니다.
    여기서 \(X_i\) 는 uniform distribution을 갖는 PDF에서 가져오게 됩니다.
    Uniform distribution를 가정하는 Basic Monte Carlo Integration을 사용합니다.
    즉 \(X_i\) 는 uniform distribution으로 가져오게됩니다.
    \(\langle F^N \rangle = (b-a) \frac{1}{N} \sum^{N}_{i=1} f(X_i)\)
\[\langle F^N \rangle = \frac{\pi/2}{N} \sum^{N-1}_{i=0} sin(X_i)\]

두번째 General Monte Carlo에 대해서..

  • 두번째 PDF의 \(X_i\) 를 구하기 위해서 먼저 CDF를 구합니다.
\[CDF(x < \mu) = \int^{\mu}_{0} \frac{8x}{\pi^2} = \left[ \frac{4x^2}{\pi^2} \right]^{\mu}_{0} = \frac{4\mu^2}{\pi^2} - 0\]
  • 이후 inverse CDF를 해줍니다.
    CDF를 통해서 x보다 작거나 같을 확률을 얻을 수 있습니다.
    Inverse CDF를 통해서는 반대로 확률 \(p\) 가 주어지면 상응하는 \(x\) 값을 알아냅니다.
\[\begin{align} CDF(x < \mu) &= \frac{4x^2}{\pi^2} \\ x^2 &= \frac{\pi^2}{4} CDF(x < \mu) \\ x &= \frac{\pi}{2} \sqrt{CDF(x < \mu)} \end{align}\]
  • 궁극적으로 두번째 PDF의 경우 General Monte Carlo를 사용합니다.
    \(X_i\) 는 위의 inverse CDF에서 나온것을 사용합니다.
    아래공식에서 PDF는 \(\frac{8X_i}{\pi^2}\) 를 가르킵니다.
\[\langle F^N \rangle = \frac{1}{N} \sum^{N-1}_{i=0} \frac{f(x_i)}{pdf(x_i)}\] 
import numpy as np
from sklearn.metrics import mean_squared_error

N = 16

x = np.arange(0, np.pi/2, 0.001)

def train(N):
    sum_uniform = 0
    sum_importance = 0
    for i in range(N):
        rand = np.random.rand(1)
        sum_uniform += np.sin(rand * np.pi * 0.5)

        x_i = np.sqrt(rand) * np.pi * 0.5
        sum_importance += np.sin(x_i)/ ((8 * x_i) / (np.pi**2))

    sum_uniform *= (np.pi * 0.5)/N
    sum_importance *= 1/N
    return sum_uniform[0], sum_importance[0]


for i in range(10):
    uniform, importance = train(N)
    a = np.abs(1-uniform)
    b = np.abs(1-importance)
    print(f'Uniform error:{a:<8.1%} Importance error:{b:<8.1%}'
          f'Uniform:{uniform:<8.3} Importance:{importance:<8.3}' )

아래는 코드의 결과입니다.

Uniform error:0.3%     Importance error:0.5%    Uniform:0.997    Importance:1.01
Uniform error:26.2%    Importance error:5.9%    Uniform:0.738    Importance:1.06
Uniform error:6.0%     Importance error:1.8%    Uniform:0.94     Importance:1.02
Uniform error:8.7%     Importance error:2.0%    Uniform:1.09     Importance:0.98
Uniform error:3.6%     Importance error:1.1%    Uniform:0.964    Importance:1.01
Uniform error:3.5%     Importance error:0.4%    Uniform:0.965    Importance:1.0
Uniform error:3.9%     Importance error:1.7%    Uniform:1.04     Importance:0.983
Uniform error:1.2%     Importance error:1.5%    Uniform:1.01     Importance:0.985
Uniform error:5.4%     Importance error:0.5%    Uniform:1.05     Importance:0.995
Uniform error:0.9%     Importance error:0.8%    Uniform:1.01     Importance:0.992

결론

integral \(f(X)\) 에 대해서 알고 있다면

  • integral \(f(X)\) 와 유사한 pdf를 사용하여 variance를 낮춘다.

integral \(f(X)\) 에 대해서 모르고 있다면

  • 전혀 알수 없다면 uniform distribution을 사용한다.