[Note] Prerequisites

Expected Value of Discrete Random Variable

Discrete random variable \(X\) 를 \(f\) 확률의 함수로 \(S\) 에서 어떤 값을 꺼낸다면 \(E(X)\) (expected valud of \(X\) 라고 함) 는 다음과 같습니다.

\[E(X) = \sum_{i = 1} x_i p_i\]
  • \(X\) : Discrete random variable
  • \(p_i\) : 각각의 random variable \(x_i\) 의 확률이며, 위키피디아에서는 \(f(x)\) 를 사용하여 probability density function으로 표현하기도 한다.
  • \(E(X)\) : weighted avarage of the values \(X\)

Expected Value of Continuous Random Variable

Continuous random variable \(Y = f(X)\) 에 대한 expected value는 다음과 같습니다.

\[\int f(x)\ pdf(x)\ dx\]

Example. 예를 들어서 주사위를 굴렸을때의 expected value의 값은 다음과 같습니다.

\[\begin{align} E(X) &= 1*P(x=1) + 2*P(x=2) + 3*P(x=3) + 4*P(x=4) + 5*P(x=5) + 6*P(x=6) \\ &= 1 * \frac{1}{6} + 2 * \frac{1}{6} + 3 * \frac{1}{6} + 4 * \frac{1}{6} + 5 * \frac{1}{6} + 6 * \frac{1}{6} \\ &= 3.5 \end{align}\]

따라서 expected value \(E(X)\) 는 3.5 입니다.

Expected Value Rules

  • Random variables 합의 expected value 는 expected values의 합과 동일합니다.
\[E\left[ \sum_{i} Y_i \right] = \sum_{i} E[Y_i]\]
  • 상수는 다음과 같이 처리 할수 있습니다. (a, b는 상수)
\[E[aX + b] = aE[X] + b\] \[E[aY] = aE[Y]\]

Variance

\[\begin{align} \sigma^2[X] &= E[ (X - E[X])^2] \\ &= E[X^2] - E[X]^2 \end{align}\]

상수는 다음과 같이 빠질수 있습니다.

\[E[aY] = aE[Y]\] \[\sigma^2[aY] = a^2 \sigma^2[Y]\]

또한 random variables이 uncorrelated이라면 summation은 variance를 갖고 있을수 있습니다.

\[\sigma^2 \left[ \sum_i Y_i \right] = \sum_i \sigma^2 [Y_i]\]

The Law of Large Numbers

  • The Law of Large Numbers : Sample size 가 증가할수록 population의 평균값에 가까워진다는 뜻으로.. 예를 들어서 동전 던지기를 대략 1,000,000번 던지면 앞면 뒷면이 나올 확률이 1:1로 거의 유사하게 나올 것 입니다. 하지만 10번정도밖에 안 던지면 1:1이 아닌 3:7 또는 2:8처럼 모수와 전혀 다른 비율로 나올 것 입니다.

  • 즉.. 여러번의 experiments (또는 trials) 를 거치고 난뒤의 평균값은 expected value 와 점점 가까워지게 될 것입니다.

Basic Monte Carlo Method

Intuition

One-dimensional function \(f(x)\) 를 a부터 b까지 integrate한다고 basic Monte Carlo integration은 다음과 같습니다.

\[F = \int^b_a f(x)\ dx\]

잘 알다시피, Integration은 함수의 curve아래의 면적을 구합니다. (Fgure 1)
만약 random value x 를 하나 선택한뒤 \(f(x) * (b-a)\) 를 하게 되면 Figure 2 처럼 직사각형 형태를 면적으로 구하게 됩니다.

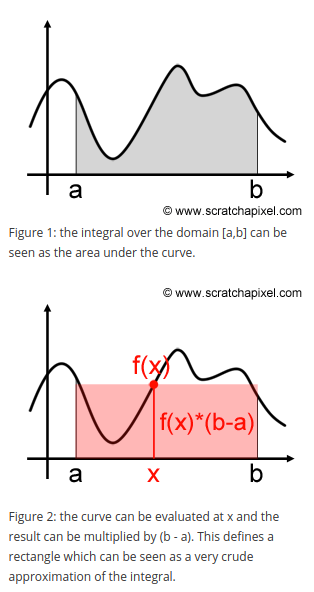
적당한 값을 찾아서 직사각형의 넓이를 구한다면 조잡하지만 curve아래의 정확한 면적을 approximate할수 있게 됩니다.
하지만 만약 \(x_1\) 을 선택하게 된다면 면적을 너무 좁게 볼 것이고, \(x_2\) 로 잡으면 면적을 너무 크게 잡게 될 것입니다.

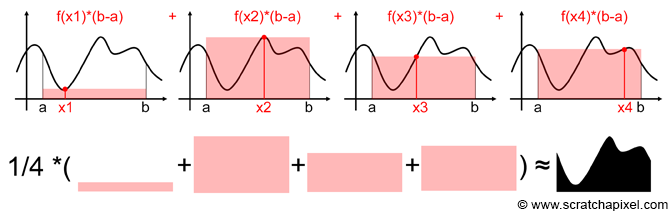
한번에 정확한 면적을 구할수는 없지만, 여러번의 random points를 잡아서 계속해서 직사각형의 면적을 구하고, 평균을 구하면 실제 curve아래의 면적과 유사해질것입니다. 포인트는 samples의 갯수가 늘어날수록 좀 더 정확한 approximation 을 할 수 있게 됩니다.

Basic Monte Carlo

위의 아이디어처럼 samples (직사각형)의 갯수가 늘어나면 날수록 integral 결과값에 approximate한다는 것을 수식화하면 다음과 같습니다.

\[\langle F^N \rangle = (b-a) \frac{1}{N} \sum^{N-1}_{i=0} f(X_i)\]
  • \(N\) : Sample의 갯수
  • \(f(X_i)\) : 위의 예제에서 직사각형의 높이
  • \(b-a\) : 위의 예제에서 직사각형의 가로길이
  • \(\frac{1}{N} \sum^{N}_{i=1} f(X_i)\) : 즉 y값의 평균을 sample로 부터 구해서 \((b-a)\)와 곱하게 되면 curve아래의 면적을 approximate할 수 있게 된다.
  • \(\langle S \rangle\) : 위키피디아 에 따르면 S안의 subgroup의 평균값을 가르킵니다. \(\langle F^N \rangle\) 는 즉 N개의 samples들의 평균값을 뜻하며 \(\bar{X}_n\) 같은 notation과 같은 의미입니다.

  • Random point: a와 b사이의 random point는 0~1사이의 random값을 numpy로 뽑고 그 랜덤값을 (a-b) 에 곱하면 됩니다.

  • Uniformly Distributed Random Value
    \(x_i = U(b-a)\) \(U\) 는 uniformly distributed 라는 뜻으로, \(b-a\) 의 값중에서 모두 동일한 확률로 sampling하겠다는 뜻

  • PDF : Probability Density Function의 경우 동일한 확률(equiprobability)로 뽑혔기 때문에 \(\frac{1}{b-a}\) 이다.
    만약 discrete 데이터이라면 \(\frac{1}{\text{total number of outcomes}}\) 하면되나, 여기에서는 continuous 데이터이기 때문에 1에다 interval [a, b] 를 나누게 된다.

증명

The law of large number에 따르면, sample들의 평균 \(\langle F^N \rangle\) 은 sample 의 갯수 \(N\) 이 많아질수록 실제 curve 아래의 면적 F 와 동일진다고 봅니다.
아래 공식에서 확률은 1이라는 뜻은 “맞다” 라는 뜻으로 보면 됩니다.

\[Pr \left(\lim_{N \to \infty} \langle F^N \rangle = F \right) = 1\]

이때 \(\langle F^N \rangle\) 은 random variable 이며, 증명은 다음과 같습니다.

\[\begin{align} E[ \langle F^N \rangle ] &= E \left[ (b-a) \frac{1}{N} \sum^{N-1}_{i=0} f(x_i) \right] & [1] \\ &= (b-a) \frac{1}{N} \sum^{N-1}_{i=0} E[f(x_i)] & [2] \\ &= (b-a) \frac{1}{N} \sum^{N-1}_{i=0} \int^b_a f(x) pdf(x)\ dx & [3] \\ &= \frac{1}{N} \sum^{N}_{i=1} \int^b_a f(x)\ dx & [4] \\ &= \int^b_a f(x)\ dx & [5] \\ &= F & [6] \end{align}\]
  • [1] : basic monte carlo를 적용하며, 해당 공식은 uniform distribution에만 적용될 수 있다.
  • [2] : expectation은 상수를 밖으로 뺄수 있으며, summation 안쪽으로 들어올수 있다.
  • [3] : continuous random variable에 대한 expectation으로 바꿔준다.
  • [4] : pdf는 continuous data이기 때문에 \(\frac{1}{b-a}\) 이며, 이는 앞쪽의 \((b-a)\) 를 상쇄시킨다.
    summation은 \(\sum^{N-1}_{i=0} = \sum^{N}_{i=1}\) 이다.
  • [5] : \(\sum^N_{i=1} I\) 가 있다면 \(N * I\) 와 같게 된다.

Multidimensional Integration

위의 Basic Monte Carlo의 경우 PDF가 오직 uniform일때만 가능합니다.
만약 random variable \(X\) 의 arbitrary PDF라면, 다음과 같이 공식화 할 수 있습니다.
위에거는 외울 필요가 없지만, 아래것은 외워야 합니다.

\[\langle F^N \rangle = \frac{1}{N} \sum^{N-1}_{i=0} \frac{f(x_i)}{pdf(x_i)}\]

위의 generalized estimator는 다음과 같은 expected value를 갖습니다.

\[\begin{align} E[\langle F^N \rangle] &= E \left[ \frac{1}{N} \sum^{N-1}_{i=0} \frac{f(X_i)}{pdf(X_i)} \right] &[1] \\ &= \frac{1}{N} \sum^{N-1}_{i=0} E \left[ \frac{f(X_i)}{pdf(X_i)} \right] &[2] \\ &= \frac{1}{N} \sum^{N-1}_{i=0} \int_{\Omega} \frac{f(x)}{pdf(x)} pdf(x)\ dx &[3] \\ &= \frac{1}{N} \sum^{N-1}_{i=0} \int_{\Omega} f(x) \ dx &[4] \\ &= \int_{\Omega} f(x) \ dx &[5] \\ &= F \end{align}\]
  • \(\int_\Omega\) : integrating을 하려는 region을 뜻한다. 1-dimension일때는 line, 2-dimensions은 area이고, 3-dimensions은 volumn을 생각하면 된다.

Monte Carlo Estimator의 convergence rate 는 \(O(\sqrt{N})\) 입니다.
Convergence rate를 제외하고도 기존 numerical integration techniques와 비교하여 장점은 multiple dimensions 으로 확장이 가능합니다.
Deterministic Quadrature techniques 경우 \(N^d\) samples이 d-dimensional integral을 위해서 필요로 합니다.
반면 Monte Carlo techniques의 경우 samples의 갯수는 정해져 있지 않습니다. (상황에 따라서 다르게 쓰면 됨)

References

  • https://cs.dartmouth.edu/~wjarosz/publications/dissertation/appendixA.pdf
  • https://www.scratchapixel.com/lessons/mathematics-physics-for-computer-graphics/monte-carlo-methods-in-practice/monte-carlo-integration