Distribution Estimation - Fitting Probability Distribution
Introduction
어떤 데이터가 있을때, 어떤 분포를 갖고 있는지 알아야 할 때가 있습니다.
Python을 통해서 가장 fitting이 잘되는 분포를 찾아내는 방법을 코드로 알아보도록 하겠습니다.
Code
Fitting Normal Distribution
예를 들어서 다음과 같은 random normal distribution을 생성합니다.
import numpy as np
import pandas as pd
from scipy import stats
import seaborn as sns
samples = stats.norm.rvs(loc=2, scale=1.5, size=1500) + 12 # 랜덤 생성
sns.distplot(samples, bins=30)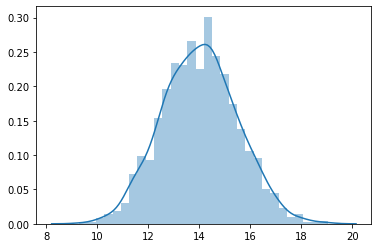
해당 데이터가 normal distribution이라고 가정했을때, 정규 분포를 만드는데 필요한 평균 그리고 표준편차는 다음과 같이 알아 낼 수 있습니다.
mean, std = stats.norm.fit(samples)
print('mean:', mean, 'std:', std)
# mean: 14.01402996451365 std: 1.478063852858123위에서 구한 평균 그리고 표준편차를 이용해서 정규분포의 pdf를 시각화 하면,
samples 데이터와 일치하는 정규분포를 그릴수 있습니다.
x = np.linspace(-3, 7, 100) # 위의 평균과 standard deviation을 고려해서 생성
pdf_fitted = stats.norm.pdf(x, loc=mean, scale=std)
pdf = stats.norm.pdf(x)
plot(x, pdf_fitted, 'r-', label='pdf_fitted')
hist(samples, bins=30, normed=1, alpha=.5)
legend()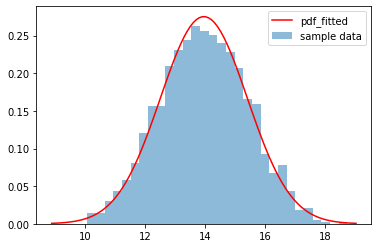
모든 분포에 사용가능한 형태의 함수
위에서 봤듯이 Scipy에서 분포마다 fit이라는 함수를 제공하고, 이를 통해서 데이터에 최대한 데이터를 맞추게 됩니다.
좀 더 공통적으로 사용하려면 아래의 함수를 사용하면 됩니다.
def estimate_distribution(data, dist_name, x_size=100):
dist = getattr(stats, dist_name)
params = dist.fit(data)
mean = params[-2]
std = params[-1]
n = data.shape[0]
x = np.linspace(mean-std*3, mean+std*3, x_size)
fitted_pdf = dist.pdf(x, *params[:-2], loc=mean, scale=std)
return x, params, fitted_pdf
x, params, fitted_pdf = estimate_distribution(samples, 'norm')
sns.lineplot(x, pdf_fitted, color='red', label='pdf_fitted')
sns.distplot(samples, bins=30, norm_hist=True, label='original')
legend()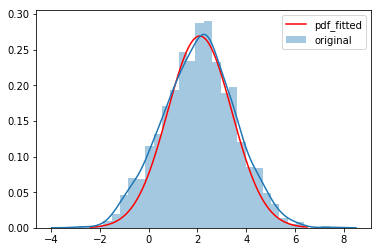
Beta Distribution
samples = stats.beta.rvs(1, 1.5, loc=2, scale=1.5, size=1500) # 랜덤 생성
x, params, fitted_pdf = estimate_distribution(samples, 'beta')
sns.distplot(samples, bins=30, norm_hist=True)
sns.lineplot(x, fitted_pdf, color='red', label='pdf_fitted')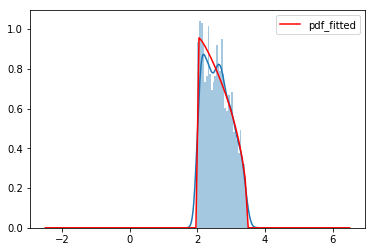
Gamma Distribution
samples = stats.gamma.rvs(1.2 ,loc=4, scale=1.5, size=1500) + 24 # 랜덤 생성
x, params, fitted_pdf = estimate_distribution(samples, 'gamma')
sns.distplot(samples, bins=30, norm_hist=False)
sns.lineplot(x, fitted_pdf, color='red', label='pdf_fitted')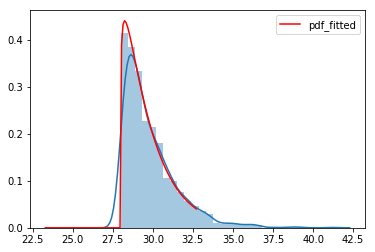
Supported Distributions from Scipy
continuous_dist = [d for d in dir(stats) if isinstance(getattr(stats, d), stats.rv_continuous)]
continuous_dist
['alpha',
'anglit',
'arcsine',
'argus',
'beta',
'betaprime',
'bradford',
'burr',
'burr12',
'cauchy',
'chi',
'chi2',
'cosine',
'crystalball',
'dgamma',
'dweibull',
'erlang',
'expon',
'exponnorm',
'exponpow',
'exponweib',
'f',
'fatiguelife',
'fisk',
'foldcauchy',
'foldnorm',
'frechet_l',
'frechet_r',
'gamma',
'gausshyper',
'genexpon',
'genextreme',
'gengamma',
'genhalflogistic',
'genlogistic',
'gennorm',
'genpareto',
'gilbrat',
'gompertz',
'gumbel_l',
'gumbel_r',
'halfcauchy',
'halfgennorm',
'halflogistic',
'halfnorm',
'hypsecant',
'invgamma',
'invgauss',
'invweibull',
'johnsonsb',
'johnsonsu',
'kappa3',
'kappa4',
'ksone',
'kstwobign',
'laplace',
'levy',
'levy_l',
'levy_stable',
'loggamma',
'logistic',
'loglaplace',
'lognorm',
'lomax',
'maxwell',
'mielke',
'moyal',
'nakagami',
'ncf',
'nct',
'ncx2',
'norm',
'norminvgauss',
'pareto',
'pearson3',
'powerlaw',
'powerlognorm',
'powernorm',
'rayleigh',
'rdist',
'recipinvgauss',
'reciprocal',
'rice',
'semicircular',
'skewnorm',
't',
'trapz',
'triang',
'truncexpon',
'truncnorm',
'tukeylambda',
'uniform',
'vonmises',
'vonmises_line',
'wald',
'weibull_max',
'weibull_min',
'wrapcauchy']discrete_dist = [d for d in dir(stats) if isinstance(getattr(stats, d), stats.rv_discrete)]
['bernoulli',
'binom',
'boltzmann',
'dlaplace',
'geom',
'hypergeom',
'logser',
'nbinom',
'planck',
'poisson',
'randint',
'skellam',
'yulesimon',
'zipf']