• Introduction
• Anova
  • Grand Mean
  • Null Hypothesis
  • Between Group Variability
  • Within-Group Variability
  • Degree of Freedom
  • F Test
• One Way ANOVA
  • Boxplot 을 통한 분석
  • With Scipy
  • with Statsmodel

Nathan Dumlao

Introduction

ANOVA는 Analysis of Variance의 약자로서, 2개 이상의 그룹의 평균을 비교하고자 할때 Anova를 사용합니다.
T-test와 유사한데 차이는 T-test는 2개의 그룹일때만 사용하고, 2개 이상일때는 ANOVA를 사용합니다.

• Tests
  • Continuous VS Category : ANOVA 사용
  • Category VS Category : Chi-sqaure test 사용
• Effect Size (얼마나 관련성이 있는지..)
  • Continous VS Category: intraclass correlation 사용
  • Category VS Category: Cramer’s V 사용
• One-way ANOVA
  • 모든 그룹의 평균값은 동일한가? (예. 연령별 (20대, 30대, 40대, 50대) 에서 커피에 대한 선호도 차이 유무를 검정
  • t-test와 유사하지만, 2개 이상의 그룹을 비교할때 사용할 수 있다. (t-test는 2개만 가능)

Anova

Grand Mean

ANOVA에서는 2종류의 평균값이 사용이 됩니다.
첫번째는 각 그룹들의 표본평균 \(\mu_1, \mu_2, \mu_3, ...\) 그리고 grand mean \(\mu\) 를 사용합니다.
grand mean은 각각의 표본평균들에 대한 평균값이라고 보면 됩니다.

Null Hypothesis

• \(H_0\) : \(\mu_1 = \mu_2 = .. = \mu_k\) 즉 귀무가설은 모든 그룹의 평균은 정확하게 일치한다 있다.
• \(H_A\) : \(\mu_l \ne \mu_m\) : 최소한 한개의 그룹은 \(\mu_i\) 는 나머지 그룹과 다은 평균값을 갖고 있다.

\(\mu\) 는 해당 그룹의 평균이고, k는 그룹의 갯수입니다.
\(\mu_l\) 그리고 \(\mu_m\) 은 전체 샘플 중에 아무거나 특정 표본평균을 뜻 합니다.

Between Group Variability

• 서로 다른 두개의 그룹을 SS 로 표현을 합니다. SS는 Sum of squares의 약자.
• 만약 각 그룹간의 표본평균이 서로 가깝다면, Grand Mean 과의 차이도 작을 것 입니다.
• \(n_i\) 는 각 그룹의 갯수를 사용해서 각각의 제곱편차(squared deviation)에 weight값으로 사용을 합니다.

쉽게 공식을 풀어 쓰면 다음과 같습니다.

아래의 두 표본의 분포를 보면, 서로 겹치는 부분이 있습니다. 각각의 표본평균과 grand mean의 차이는 크지 않을 것 입니다.

def plot_normal_dist(means, sigmas):
    for i, (sample_mean, sigma) in enumerate(zip(means, sigmas)):
        normal_data = np.random.normal(sample_mean, scale=sigma, size=100)
        sns.distplot(normal_data)

means = [4, 3.5]
sigmas = [0.2, 0.5]
plot_normal_dist(means, sigmas)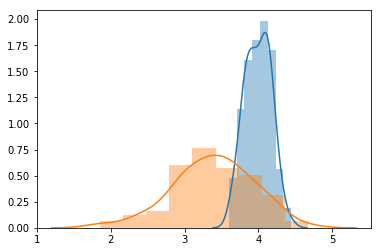

반면에 아래의 두 표본분포를 서로 크게 떨어져 있습니다. 이 경우 각각의 표본 평균과 grand mean은 서로 크게 차이가 날 것입니다.

plot_normal_dist([2, 5], [0.2, 0.3])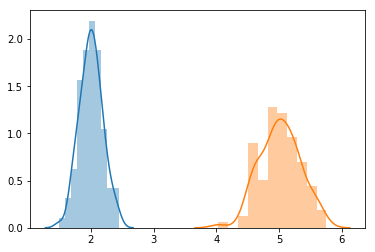

이렇게 각 표본분포간의 차이를 Between-group variability 라고 합니다.

between-group variability의 경우 자유도는 표본 평균의 갯수 k에 -1 을 한 것입니다.

• k : 그룹의 갯수

Within-Group Variability

\(n_{1i}\) 라는 뜻은 첫번째 샘플에서의 i번째의 값을 의미 합니다.
\(n_{2i}\) 라는 뜻은 두번째 샘플에서의 i번째의 값을 의미 합니다.
\(n_{ji}\) 라는 뜻은 j번째 샘플에서의 i번째 값을 의미 합니다.

예를 들어서 아래 세개의 표본에 대한 분포를 그렸습니다.
각 그룹들이 옆으로 더 퍼질수록 (variability), 각 그룹들의 분포는 서로 겹치게 되고, 하나의 큰 population이 되게 됩니다.

plot_normal_dist([1, 20, 40], [7, 7, 7])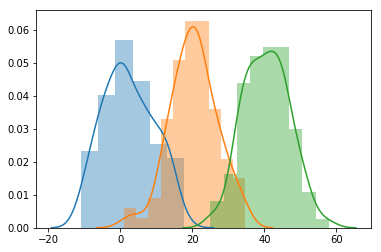

이번에는 위와 동일한 평균값을 갖고 있지만, 적은 변동성 (variability)을 갖고 있는 분포를 보도록 하겠습니다.
위와 동일하게 샘플들간의 표본평균은 동일하지만, 서로 완전히 다른 population에 종속이 되어 있습니다.

plot_normal_dist([1, 20, 40], [2, 2, 2])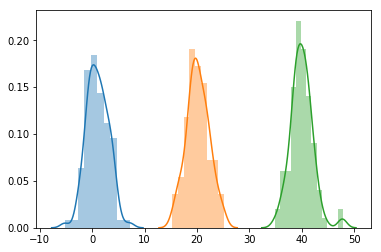

위와 같이 각 샘플안에서의 variation을 Within-group Variation이라고 합니다.
즉 Between-group variability는 각 샘플들 사이의 표본평균의 차를 구했다면..
Within-group variation에서는 각각의 샘플들 마다 존재하는 편차를 구하게 됩니다.

Between-group variability에서 했듯이, 제곱편차의 합을 degrees of freedom으로 나누어 줄수 있습니다.
이렇게 나누어 주면 좀더 덜 편향된 (less biased) estimator를 구할 수 있습니다.

Within-group variability의 degrees of freedom은 전체 샘플 크기들의 합 (sum of the sample sizes) N 에다 샘플듯의 갯수 k 를 빼주게 됩니다.

• MS: mean sum of square
• N : 전체 데이터 갯수
• k : 샘플들의 갯수

Degree of Freedom

각 공식별 degree of freedoms은 다음과 같이 정의 할 수 있습니다.

• \(DOF(SS_{between})\) = \(k -1\)
• \(DOF(SS_{within})\) = \(N - k\)
• \(DOF(total)\) = \(N - 1\)

F Test

독립변수와 종속변수 사이의 관계성을 테스트하기 위해서는 F distribution이 사용이 됩니다.

• \(MS_{\text{between}}\) : mean sum of squares due to treatment
• \(MS_{\text{within}}\) : mean sum of squares due to error

표본평균들간의 차이를 나타낸 것을 F-Ratio 라고 합니다.
F-Ratio의 값이 1 또는 그 이하라면, 표본평균들은 서로 유사하다고 볼수 있으며,
표본평균들이 모두 모평균과 동일하다는 귀무가설이 맞게 됩니다..
만약 F-Ratio의 값이 매우 높다면, 귀무가설은 기각이 됩니다.

앞서 언급했듯이 between-group variability(그룹 간 변동성) 증가할수록, 표본평균들간의 거리는 서로 더 멀리 떨어져 있다고 볼 수 있습니다.
즉 멀어지면 멀어질수록 다른 모집단에 속해 있을 가능성이 큽니다.

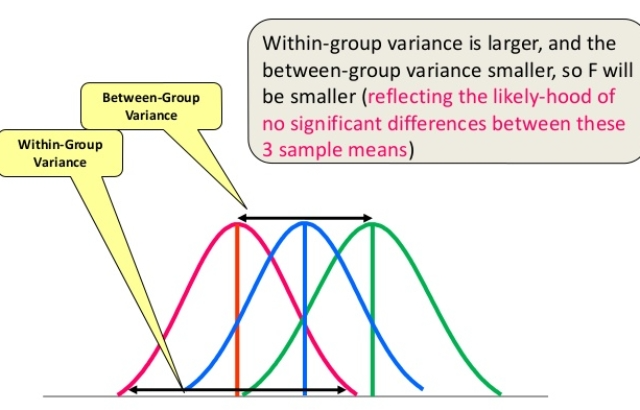
Source: Dr. Asim’s Anatomy Cafe

z 그리고 t-distributions과는 다르게, F-distribution은 negative value가 없습니다.
이유는 between group이나 within group 모두 각 편차를 제곱(squaring each deviation)하기 때문입니다.

따라서 아래 그래프에서 보듯이 임계 영역(critical region)은 오른쪽 꼬리(right tail)에 한군데 존재합니다.

만약 F-statistic값이 해당 임계 영역안에 있다면 서로간의 표본평균들은 매우 다르기 때문에 귀무가설을 기각할 수 있습니다.

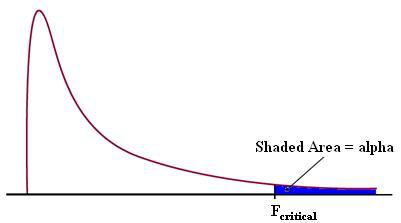
Source: Statistics How To

임계 영역을 나누는 critical value를 찾아야 하는데, 이때 F-table을 사용하게 됩니다.

One Way ANOVA

예제를 갖고서 설명을 하겠습니다.

그룹 X, Y, Z그룹으로 나뉘어 지며, 공부 방법에 따른 성적이라고 생각하면 됩니다.

data = pd.DataFrame([[7, 9, 5, 8, 6, 8, 6, 10, 7, 4], 
                     [4, 3, 6, 2, 7, 5, 5, 4, 1, 3],
                     [6, 1, 3, 5, 3, 4, 6, 5, 7, 3]]).T

data.columns = ('X', 'Y', 'Z')

print('[표본평균]')
print(data.mean(axis=0))
print()

print('[Grand Mean]')
print(data.mean(axis=0).mean())

[표본평균]
X    7.0
Y    4.0
Z    4.3
dtype: float64

[Grand Mean]
5.1000000000000005

• 각 그룹의 표본평균: \(\mu_1 = 7\), \(\mu_2 = 4\), \(\mu_3 = 4.3\)
• 전체 평균 (Grand Mean): \(\mu = 5.1\)

Boxplot 을 통한 분석

간단하게는 boxplot을 통해서 대략의 인싸이트를 얻을 수 있습니다.

아래에서도 언급하겠지만, boxplot만 갖고서 결론을 내리기에는 부족합니다.

sns.boxplot(data=data)
sns.swarmplot(data=data, color='.2')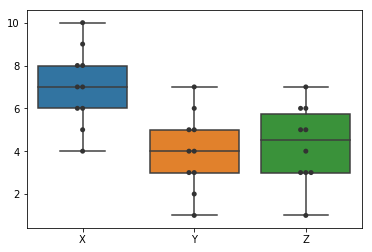

Boxplot을 통해서 분산분석을 하는 것은 꽤 유용합니다.
다만 boxplot만 보고서 판단은 할 수가 없습니다.
\(SS_{between}\) 에서 보면, n * square of deviation 을 하게 되는데.. 여기서 n값이 weight값으로 사용이 됩니다.
즉 boxplot자체에는 각 샘플마다 얼마나 중요도가 있는지 알 수가 없으며,
또한 각 표본평균들간에 실제로 얼마나 차이가 나고 의미가 있는지, 분산이 큰것과는 어떤 관계가 있는지 등등 유의성을 알 수가 없습니다.
이 경우 일원분산분석이나 이원분산분석등을 사용하게 됩니다.

With Scipy

Scipy를 이용해서 두개 이상의 그룹이 동일한 모평균을 갖고 있다는 귀무가설을 테스트 할 수 있습니다.
이때 P-value가 유효하기 위해서는 다음의 가정이 충족되어야 합니다.

• 표본들은 모두 독립적이다.
• 각각의 표본들은 정규분포를 따른다
• 모든 그룹들의 모표준편차 (population standard deviations of the groups) 는 모두 동일하다

만약 위의 가정들이 맞지 않는다면, Kruskal Wallis H-test 같은 다른 방법을 사용해야 합니다.

from scipy import stats

F_statistic, p_value = stats.f_oneway(data['X'], data['Y'], data['Z'])
print('F={0:.4f}, p={1:.5f}'.format(F_statistic, p_value))

F=8.1809, p=0.00167

위에서 P-value 값이 0.05보다 작기 때문에 통계적으로 유의미함을 나타냅니다.
또한 F-statistic값이 8.18이라는 뜻은 between-group variance가 within-group variance보다 약 8.18배 더 크다는 뜻입니다.
결론적으로 표본평균은 모두 동일하다는 귀무가설을 기각할수 있습니다.

Scipy에서 제공하는 라이브러리의 문제점은 F-critical value 를 따로 계산을 해주어야 합니다.
이때 scipy.stats.f 안의 ppf를 사용해서 critical value를 계산할 수 있습니다.

from scipy.stats import f, norm

N = data.shape[0] # 10
k = data.shape[1] # 3

dfn = k - 1 # degree of freedom numerator -> k - 1 
dfd = N - k # degree of freedom denominator -> N - K 
critical_value = f.ppf(q=0.95, dfn=dfn, dfd=dfd)

print('Degree of freedom Numerator  : {0} - 1 = {1}'.format(k, dfn) )
print('Degree of freedom Denominator: {0} - {1} = {2}'.format(N, k, dfd))
print('Critical Value (rejection)   :', critical_value)

Degree of freedom Numerator  : 3 - 1 = 2
Degree of freedom Denominator: 10 - 3 = 7
Critical Value (rejection)   : 4.73741412777588

def plot_f_distribution(dfn, dfd, f_value=None):
    critical_value = f.ppf(q=.95, dfn=dfn, dfd=dfd)
    mean, var, skew, kurt = f.stats(dfn, dfd, moments='mvsk')
    x = np.linspace(f.ppf(0.01, dfn, dfd), f.ppf(0.99, dfn, dfd), 100)
    
    # Plotting
    plt.plot(x, f.pdf(x, dfn, dfd), alpha=0.6, label='X~ F({0}, {1})'.format(dfn, dfd))
    plt.vlines(critical_value, 0.0, 1.0, linestyles='dashdot', 
               label='Crit. Value: {:.2f}'.format(critical_value), color='red')
    
    if f_value is not None:
        plt.vlines(f_value, 0., 1., label='F-value')
    plt.legend()
    plt.grid()
    

plot_f_distribution(dfn, dfd, 8.1809)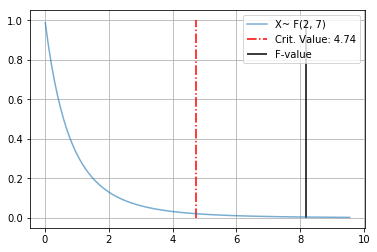

with Statsmodel

import statsmodels.api as sm
from statsmodels.formula.api import ols

moore = sm.datasets.get_rdataset("Moore", "carData", cache=True).data
moore.rename(columns={'partner.status': 'partner_status'}, inplace=True) # make name pythonic
display(moore.head())

moore_lm = ols('conformity ~ C(fcategory, Sum) * C(partner_status, Sum)', data=moore).fit()
display(moore_lm.summary())

sm.stats.anova_lm(moore_lm, typ=2)

MSB = 11.6147 / 2.
MSE = 817.763961/39.

print('F-statistic for fcategory:', MSB/MSE)
print('F-statistic for partner_status:', (212.213778/1.)/MSE)
print('F-statistic for fcategory + partner_status:', (175.488928/2.)/MSE)

F-statistic for fcategory: 0.276958463323624
F-statistic for partner_status: 10.120692200570085
F-statistic for fcategory + partner_status: 4.1846232644140695