Humoungous - Intermediate Probability
- Binomial Probability Distribution
- Poisson Probability Distribution (푸아슨 분포)
- Normal Distribution & Z-Score - {:.} Normal Distribution in Python
Binomial Probability Distribution
- Binomial의 이름에서 알 수 있듯이, 2개의 결과값을 갖는다 (주로.. 성공 또는 실패)
| n | 시도 횟수 | 고정값 fixed number of trials |
| r | 성공 횟수 | 변수 |
| p | 성공 확률 | 상수 - 즉 고정값 |
| q | 실패 확률 | 상수 - 즉 고정값 |
Q. 동전을 6번 던져을때 정확하게 두번 heads가 나오는 확률은?
(23.4%의 확률로 정확하게 2번 heads가 나올수 있다.)
\[P(r) = \begin{pmatrix}
6 \\
2 \\
\end{pmatrix}
\frac{6*5}{2*1}(0.5)^{2}(0.5)^{4}
= 15 * 0.25 * 0.0625 = 0.234375\]
Q. 동전을 6번 던져을때의 평균, Variance, Standard Deviation 을 구하세요.
| Mean | \(\begin{align} \mu = np \end{align}\) | \(\mu = 6 * 0.5 = 3\) |
| Variance | \(\begin{align} \sigma^{2} = npq \end{align}\) | \(\sigma^{2} = 6 * 0.5 * 0.5 = 1.5\) |
| Standard Deviation | \(\sqrt{\sigma^{2}}\) | \(\sqrt{1.5} = 1.225\) |
Poisson Probability Distribution (푸아슨 분포)
- 특정 시간,범위,거리 동안에 (interval) 어떤 이벤트가 몇 번 일어날지 예측한다.
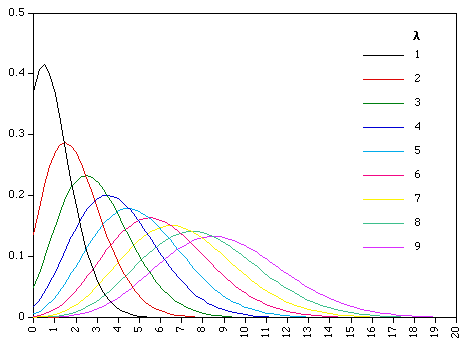
| x | interval 마다 몇번일 발생했는지 (Occurrences) |
| \(\lambda\) | interval 마다 평균 몇번이 발생했는지 (Average Occurrences); lambda라고 읽는다 |
| e | Euler’s number 2.71828… |
Q. 시간당 7명의 손님이 오는 가게에, 다음 1시간 동안 정확하게 4명의 손님이 올 확률을 계산하여라.
\[P(x) = \frac{7^{4} e^{-7}}{4!} = 0.0912\]
Q. 시간당 7명의 손님이 오는 가게의, 평균, Variance, STD를 구하세요.
| Mean | \(\mu = \lambda\) | \(\mu = 7\) |
| Variance | \(\sigma^{2} = \lambda\) | \(\sigma^{2} = 7\) |
| STD | \(\sigma = \sqrt{\sigma^{2}}\) | \(\sigma = \sqrt{7} = 2.65\) |
이때 Mean 과 Variance가 거의 동일하지 않다면, 데이터가 Poisson Distribution이 아닐수 있습니다.
Normal Distribution & Z-Score
- mean을 중심으로 Symmetric 이다.
- mean, median, 그리고 mode가 모두 같은 값이다.
- 전체 면적은 1이다.
- Bell Curve라고도 불린다.
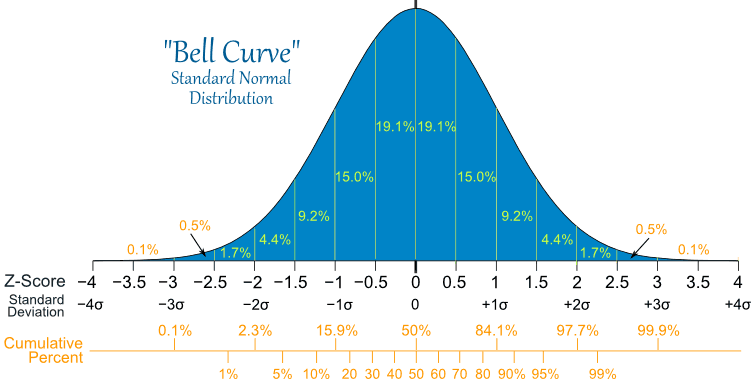
| Mean | 값이 높으면 그래프를 우측으로, 낮으면 좌측으로 움직이다. | |
| STD | 값이 눂을수록 더 넓게 분산된다. 작으면 좁은 bell-shaped 커브를 그린다. | |
| Z-Score | 특정 x와 mean사이에 STD가 몇개가 들어가는지 계산을 한다. | \(\begin{align} z_{x} = \frac{x - \mu}{\sigma} \end{align}\) |
Normal Distribution in Python
import numpy as np
from scipy import stats
data = np.random.normal(size=10000)
data.sort()
pdf = stats.norm.pdf(data, data.mean(), data.std())
plt.plot(data, pdf)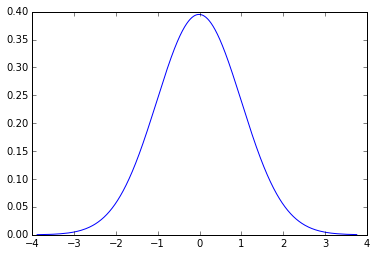
Q. 자동차가 체크포인트를 지나가는 시점이 normally distributed라고 가정하고, 평균 시간당 61 miles, 그리고 std는 시간당 4일때, 그 다음 자동차가 시간당 65마일 이하로 지나갈 확률은?
\[z = \frac{65-61}{4} = 1\]
z-score가 1값으로 나왔는데, stadard normal table에서 확인해 보면, z-score of 1.00과 mean사이의 area값은 0.3413이 나옵니다.