Improving Policy Gradients with a baseline

The problem of the PG

Policy Gradient는 다음과 같습니다. (REINFORCE Method 참고)

\[\nabla_{\theta} J(\theta) = \sum^{T}_{t=1} \nabla_{\theta} \log \pi_{\theta} (a_t | s_t) \cdot R_t\]
  1. PG는 게임이 끝날때까지 기다린 다음에 모델을 학습 가능 -> 학습 속도 저하
  2. Cumulative reward를 사용하기 때문에 0이 될 수도 있음 -> Good actions 그리고 Bad actions 이 서로 상쇄해서 0값 -> 학습 안됨
  3. Cumulative reward를 사용하기 때문에 특정 bad actions 또는 good actions을 학습하지 못함 (good actions이 많은 경우 bad actions을 압도함)

Reducing variance with Baseline

결론적으로 \(R_t\) 가 너무 큰 값이 들어오거나 작은 값이 들어오거나, stable하지 않아서 생기는 문제를 해결하는 방법으로
cumulative reward를 baseline으로 빼줌으로서 조금더 reward를 stable하게 만들어 줍니다.

\[\nabla_{\theta} J(\theta) = \sum^{T}_{t=1} \nabla_{\theta} \log \pi_{\theta} (a_t | s_t) \cdot (R_t - b(s_t))\]

직관적으로 보면 \(R_t - b(s_t)\) 를 해줌으로서 reward자체가 작아지게 되고, 당연히 gradient값도 작아지게 될 것입니다.
예를 들어서 다음과 같다고 할때..

\[\begin{align} \nabla_{\theta} \log \pi_{\theta}(a_t | s_t) &= [0.5, 0.2, 0.3] \\ R(t) &= [1000, 1001, 1002] \\ \nabla_{\theta} \log \pi_{\theta}(a_t | s_t) \cdot R(t) &= [0.5 \cdot 1000, 0.2 \cdot 1001, 0.3 \cdot 1002] \end{align}\]

해당값의 np.var([0.5*1000, 0.2*1001, 0.3*1002]) = 15524.5 이 나오게 됩니다.
즉 상당히 큰 값의 variance값이 나오게 됩니다.

만약 baseline으로 \(R_t\) 에다가 1000을 빼주게 되면 다음과 같이 되게 될 것입니다.

\[\begin{align} \nabla_{\theta} \log \pi_{\theta}(a_t | s_t) &= [0.5, 0.2, 0.3] \\ R(t) &= [0, 1, 2] \\ \nabla_{\theta} \log \pi_{\theta}(a_t | s_t) \cdot R(t) &= [0.5 \cdot 0, 0.2 \cdot 1, 0.3 \cdot 2] \\ &= 23286.8 \end{align}\]

np.var([0.5 * 0, 0.2*1, 0.3*2]) = 0.062 값이 나옵니다.
즉 작은 gradient값이 나오게 되고 stable한 학습이 가능해집니다.

Advantage Actor Critic Method

A2C 는 actor 그리고 critic 두개의 모델을 하나의 neural network에서 예측할수 있는 모델입니다.
기본적으로 actor는 어떤 action을 취할지, 그리고 critic은 action에 대해서 feedback을 주는 형태로서 기본적으로 Q-value와 연관이 깊다고 생각하면 됩니다.

Actor 그리고 Critic 모델의 구조는 다음과 같습니다.

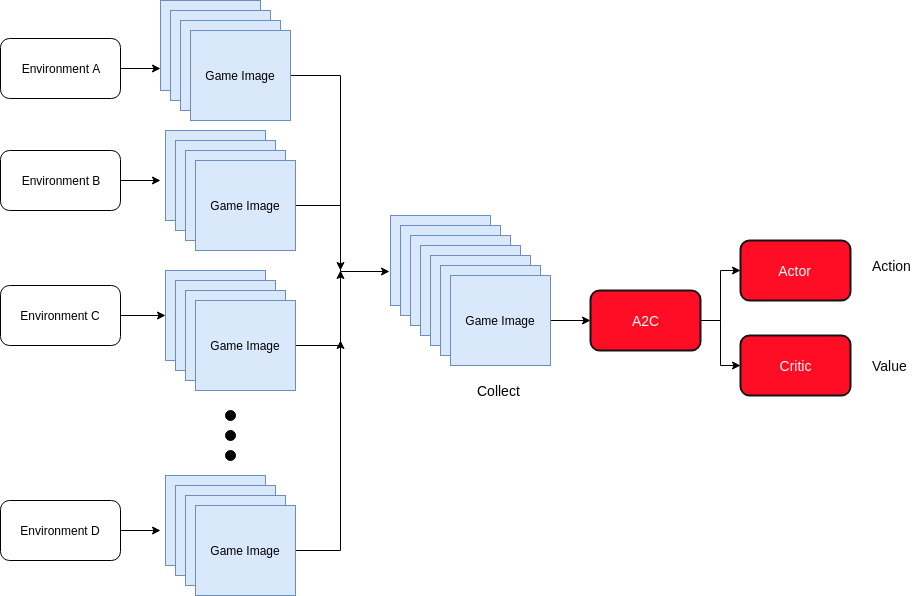
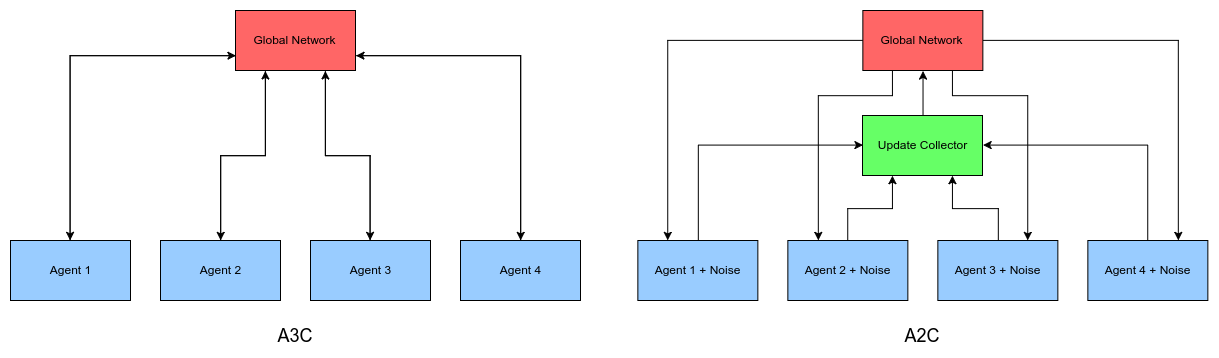
참고로 A2C와 A3C의 다른점은 environments로 부터 받아오는 부분에서
synchronous 또는 ascynchronous인지로 달라지게 됩니다.

Loss Function

\[L = L_{\pi} + c_v L_v + c_{e} L_{\text{entropy}}\]
  • L : 최종 loss value
  • \(L_{\pi}\) : policy loss
  • \(L_v\) : value loss
  • \(L_{\text{entropy}}\) : action에 대한 entropy 값
  • \(c_v\) : \(L_v\) 에 대한 가중치 값으로서 constant value (ex. 0.5)
  • \(c_{e}\) : \(L_{\text{entropy}}\) 에 대한 가중치 값으로서 constant value

Value Loss

\[L_{v} = \frac{1}{n}\sum^n_{t=1} \left[Q(s_t, a_t) - V_v(s_t) \right]^2\]
  • \(Q(s_t, a_t) = \mathbb{E} \left[ r_{t+1} + \gamma V(s_{t+1}) \right]\) 중요한 점은 baseline으로 감산하지 않으며,
    2-step, 또는 n-step 처럼 많아질 경우 공식이 달라짐 (아래 확인)
  • \(V_v(s_t)\) : critic model로 나온 output값
  • 즉 실제 Q-value와 critic으로 나온 예측값을 MSE로 loss를 만들어 낸다

Policy Loss

\[L_{\pi} = - \frac{1}{n} \sum^n_{i=1} A(a_i| s_i) \cdot \log(\pi(a_i| s_i))\]
  • \(A(s_t, a_t)\) : Advantage Function. 실제 구현은 1-step이냐 n-step이냐 또는 GAE등이냐에 따라서 구현 방법이 달라질수 있습니다. 쉽게 생각해서 baseline을 갖고 있는 q-value
  • Policy Model: actor model은 현재 state를 보고 그 다음 action \(a_{t+1}\) 을 예측합니다.
  • negative value : maximize 하는 것이기 때문에 음수값을 사용
  • \(\pi(a_i \| s_i)\) : policy network에서 나온 결과값에 softmax를 씌움 -> 해당 action값에 해당하는 확률

Policy Function

\[\pi(a_i | s_i) = softmax(output)[action]\]
  • output : 딥러닝의 output으로서 softmax하기전의 linear output
  • [action] : softmax(output) = [0.1, 0.2, 0.3, 0.4] 이고 실제 action으로 한 값이 2라면 최종값은 0.2

Advantage Function

\[A(s_t, a_t) = Q_w(s_t, a_t) - V_v (s_t)\]
  • \(Q_w(s_t, a_t)\) : Q value for an action a in state s
  • \(V(s)\) : average value of that state

V function을 baseline function으로 사용함으로서, Q value - V value 를 하게 됩니다.
즉, 특정 action을 취하는 것이 일반적으로 기대할수있는 값보다 얼마나 더 좋을가를 나타내는 것입니다.
해당 action이 해당 state에서 평균적인 action보다 얼마나 더 좋냐? 라고 물어보는 것과도 같습니다.

1-step advantage 는 다음과 같습니다.

\[A(s_t, a_t) = r_{t+1} + \gamma V_v(s_{t+1}) - V_v(s_t)\]

Pytorch Example

예를 들어서 actor model의 output은 softmax 함수로 계산을 합니다.
이후 action 1에 해당하는 확률은 0.2157인데 여기에 log(0.2157) 로 계산을 합니다.
2.5를 곱해주는 것은 바로 \(A(s_t, a_t)\) 값으로 나온 baseline Q-value 입니다.

>> output = torch.Tensor([[0.1, 0.5, 1.3, 0.2]])
>> action = torch.Tensor([[1]])
>> q_value = torch.Tensor([[2.5]])
>>
>> softmax_value = F.softmax(output, dim=-1)
tensor([[0.1446, 0.2157, 0.4800, 0.1598]])

>> category = Categorical(softmax_value)
>> actor_loss = -category.log_prob(action) * q_value
tensor([[3.8350]])

>> actor_loss.mean()
tensor(3.8350)

Policy Entropy

policy에 대한 entropy를 구하는 공식은 아래와 같습니다.

\[\begin{align} H(\pi(s)) &= - \sum^n_{k=1} \pi(s) \cdot \log \pi(s) \\ L_{entropy} &= -\frac{1}{n} \sum^n_{i=1} H(\pi(s_i)) \end{align}\]

특정 action에 대해서 확인이 없을때는 entropy값은 높아지고 loss함수의 penalty로 들어가게 됩니다.

Pytorch code로 보면 다음과 같습니다.

>> output = torch.Tensor([[0.1, 0.5, 1.3, 0.2]])
>> action = torch.Tensor([[1]])
>> q_value = torch.Tensor([[2.5]])
>>
>> softmax_value = F.softmax(output, dim=-1)
tensor([[0.1446, 0.2157, 0.4800, 0.1598]])

>> category = Categorical(softmax_value)
>> entropy = category.entropy()
tensor([1.2558])

Temporal Difference

TD(1)

궁극적으로 Monte Carlo, REINFORCE와 동일하게 episode가 끝날때까지 기다린다음에 update가 가능합니다.

\[\begin{align} V(s_t) &= V(s_t) + \alpha(G_t - V(s_t)) \\ G_t &= r_{t+1} + \gamma r_{t+2} + \gamma r_{t+3} + ... + \gamma^{T-1}r_T \end{align}\]
  • \(T\) : Terminal

TD(0)

TD(1)에서는 episode가 끝날때까지의 sum of discounted rewards \(G_t\) 를 사용했었습니다.
TD(0)의 경우는 바로 앞단계 1-step reward \(r_{t+1}\) 만 보게 됩니다.

\[V(s_t) = V(s_t) + \alpha(r_{t+1} + \gamma V(s_{t+1}) - V(s_t) )\]

TD(λ) :: Semi Gradient TD

TD(0) 와 TD(1) 의 장단점을 합쳐놓은 것이 TD(λ) 입니다.
N-Step Bootstrapping이라고도 하며 N 개의 rewards를 사용해서 업데이터를 합니다.
문제는 여러개의 rewards가 있는데 어떻게 credit assignment를 할 것인지 입니다.
여기에서 사용하는 방법이 Eligibility Traces (ET) 라고 하며,
기본적인 방법은 Recency 그리고 Frequency 에 따라서 credit assignment를 합니다.

\(z_0 = 0\) \(E_t(s) = \gamma \lambda E_{t-1}(s) + 1 (s_t = s)\)

N-Step Boostrapping

Background (MC and TD)

Monte Carlo (MC)의 경우 에피소드가 끝날때가지 기다려야 하고,
One-step temporal difference (TD)의 경우는 다로 다음 스텝까지만 기다리면 됩니다.

\[\begin{align} \text{MC | } TD(1) &= V(S_t) = V(S_t) + \alpha \left[ G_t - V(S_t) \right] \\ TD(0) &= V(S_t) = V(S_t) + \alpha \left[ R_{t+1} + \gamma V(S_{t+1}) - V(S_t) \right] \end{align}\]
  1. Monte Carlo
    • 장점: 특정 state에 bias가 줄어든다
    • 단점: high variance 문제를 겪을 수 있으며, 에피소드가 끝날때 까지 기다려야 하기 때문에 느리다
  2. Temporal Difference
    • 장점: low variance 이며, 다음 스텝 까지만 보기 때문에 효율적이다
    • 단점: 최초에 값이 매우 부정확하거나, 특정 state에 대한 bias가 심하다

N-Step Bootstrapping

MC 와 TD의 장점을 서로 합친 개념입니다.

Q function은 대략 다음과 같습니다.

\[\begin{align} Q_{\pi} &= \mathbb{E} \left[ r_0 + \gamma r_1 + \gamma^2 r_2 + ... + \gamma^T r_T \right] & \text{Monte Calro} \\ &= \mathbb{E} \left[r_0 + \gamma V_{\pi}(s_1) \right] & \text{1-step TD} \\ &= \mathbb{E} \left[r_0 + \gamma r_1 + \gamma^2 V_{\pi}(s_2) \right] & \text{2-step TD} \\ &= \mathbb{E} \left[r_0 + \gamma r_1 + \gamma^2 r_2 + \gamma^3 r_3 + ... + \gamma^n V_{\pi}(s_n) \right] & \text{n-step TD} \\ \end{align}\]

Monte Carlo

\[G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + ... + \gamma^{T-t-1}R_T\]

TD

\[G_{t:t+1} = R_{t+1} + \gamma V_t(S_{t+1})\]

2-Step return

\[G_{t:t+1} = R_{t+1} + \gamma R_{t+2} + \gamma^2 V_t(S_{t+2})\]

n-step return

\[G_{t:t+n} = R_{t+1} + \gamma R_{t+2} + ... + \gamma^{n-1} R_{t+n} + \gamma^n V_{t+n-1}(S_{t+n})\]

N-Step Implementation

N-Step 의 이슈중에 하나는 \(t\) 라는 현재시점 \(s_t\) 에서 \(a_t\) 을 취했을때 나오는
\(\text{next_reward} = r_{t+1}\) 그리고 \(\text{next_state} s_{t+1}\) 밖에 모르는 상황입니다.

문제는 N-Step을 구현하기 위해서는 미래시점의 rewards 들이 필요합니다.
즉 이런 것들.. \(r_{t+2}, r_{t+3}, ..., r_{t+n}, s_{t+n}\)

따라서 구현상에서는 time windows of size n 의 크기로 states, actions, 그리고 rewards들을 저장해놓습니다.
그리고 학습시에는 \(V_{\pi} (S_{t-n})\) 즉 t-n 시점으로 돌아가서 학습을 할 수 있습니다.

저장된 action, state, reward를 갖고서 다음의 코드처럼 구현 할 수 있습니다.

# N-Step Bootstrapping
critic_y = np.zeros(self.n_step)  # discounted rewards
_next_value = pred_next_values[-1]
for t in range(self.n_step - 1, -1, -1):
    # 1-step TD: V(s_t) r_t + \gamma V(s_{t+1}) - V(s_t)
    _next_value = rewards[t] + gamma * _next_value * (1 - dones[t])
    critic_y[t] = _next_value
actor_y = critic_y - pred_values
  • pred_next_values[-1] : Critic 모델이 예측한 가치값으로서 N-Step에서 마지막 state를 넣어서 나온 값
  • rewards : n-step rewards를 저장해놓은 list

forloop을 풀어서 적으면 다음과 같이 됩니다.

Policy Target

\[\begin{align} R_{t+1} + \gamma (R_{t+2} + \gamma (R_{t+3} + \gamma (R_{t+4} + \gamma (R_{t+5} + \gamma V(S_{t+5}))))) - V(S_{t:t+5})\\ = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \gamma^3 R_{t+4} + \gamma^4 R_{t+5} + \gamma^5 V(S_{t+5}) - V(S_{t:t+5}) \end{align}\]

Value Target

\[\begin{align} R_{t+1} + \gamma (R_{t+2} + \gamma (R_{t+3} + \gamma (R_{t+4} + \gamma (R_{t+5} + \gamma V(S_{t+5}))))))\\ = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \gamma^3 R_{t+4} + \gamma^4 R_{t+5} + \gamma^5 V(S_{t+5})) \end{align}\]
  • \(R\) : rewards[t]
  • \(\gamma\) : 0~1 사이의 값 (보통 0.99)

Generalized Advantage Estimation (GAE)

Infinite Geometric Series Formula

칸 아카데미의 Infinite Geometric Series Formula Intuition 을 참고 합니다.

아래의 공식은 GAE 수식 도출에 참고해야 합니다.

\[\begin{align} \sum^\infty_{k=0} = S_{\infty} &= \alpha r^0 + \alpha r^1 + \alpha r^2 + \alpha r^3 + ... + \alpha r^\infty \\ r S_{\infty} &= \alpha r^1 + \alpha r^2 + \alpha r^3 + \alpha r^4 + ... + \alpha r^\infty \\ S_{\infty} - r S_{\infty} &= \alpha \cdot 1 \\ S_{\infty} (1-r) &= \alpha \\ S_{\infty} &= \frac{\alpha}{1-r} \end{align}\]

아래 GAE에서 다시 설명하지만 \((1-\alpha)\) 를 TD에다가 곱하게 됩니다.
이경우 아래와 같이 모두 합한 값이 1이 되게 만들려고 하는 의도 입니다.

\[(1-r) \cdot \frac{\alpha}{1-r} = \alpha\] 
lambda_ = 0.95

print('sum method   :', sum([lambda_**i for i in range(1000)]))
print('approximation:', 1 / (1-lambda_))
sum method   : 19.999999999999982
approximation: 19.999999999999982

Generalized Advantage Estimation ( \(\lambda - \text{return}\) )

https://arxiv.org/pdf/1506.02438.pdf

Monte carlo의 경우 episode가 끝날때까지 기다려야 하기 때문에 학습 속도에 있어서 문제가 있으며,
1-step temporal difference learning의 경우 속도는 빠르지만 bias한 것이 문제가 될 수 있습니다.
그래서 N-Step Learning이 나오게 되었지만, 역시 여전히 최적의 n값을 지정하는 것은 다시 문제가 될 수 있습니다.

\(TD(\lambda)\) 는 이러한 문제를 해결하기 위해서 나온 알고리즘입니다.
기본적인 아이디어는 단 하나의 최적의 n값을 사용하는것이 아니라 모든 가능한 n-step TD의 weighted sum을 적용하는 것입니다.

먼저 advantage function을 정의하면 다음과 같습니다.

\[\text{advantage function} = A(s_t, a_t) = r_t + \gamma V(s_{t+1}) - V(s_t)\]

n-step에 따라서 advantage function의 모습은 다음과 같이 변합니다.

\[\begin{align} & A^{(1)}_t = \delta_t & &= r_t + \gamma V(s_{t+1}) - V(s_t) \\ & A^{(2)}_t = \delta_t + \gamma \delta_{t+1} & &= r_t + \gamma r_{t+1} + \gamma^2 V(s_{t+2}) - V(s_t) \\ & A^{(3)}_t = \delta_t + \gamma \delta_{t+1} + \gamma ^2 \delta_{t+2} & &= r_t + \gamma r_{t+1} + \gamma^2 r_{t+2} + \gamma^3 V(s_{t+3}) - V(s_t) \end{align}\]

최종적으로 Generalized Advantage Estimation (GAE) 는 exponentially-weighted average of n-step estimators 로 정의가 될 수 있습니다.

\[\begin{align} A_t^{GAE(\gamma,\lambda)} &= (1-\lambda)\Big(A_{t}^{(1)} + \lambda A_{t}^{(2)} + \lambda^2 A_{t}^{(3)} + \cdots \Big) \\ &= (1-\lambda)\Big(\delta_t^V + \lambda(\delta_t^V + \gamma \delta_{t+1}^V) + \lambda^2(\delta_t^V + \gamma \delta_{t+1}^V + \gamma^2 \delta_{t+2}^V)+ \cdots \Big) \\ &= (1-\lambda)\Big( \delta_t^V(1+\lambda+\lambda^2+\cdots) + \gamma\delta_{t+1}^V(\lambda+\lambda^2+\cdots) + \cdots \Big) \\ &= (1-\lambda)\left(\delta_t^V \frac{1}{1-\lambda} + \gamma \delta_{t+1}^V\frac{\lambda}{1-\lambda} + \cdots\right) \\ &= \sum_{l=0}^\infty (\gamma \lambda)^l \delta_{t+l}^{V} \end{align}\]

맨 아래쪽 공식 \(\sum_{l=0}^\infty (\gamma \lambda)^l \delta_{t+l}^{V}\) 을 보면 최종적으로 매우 간결한 공식이 나온것을 알 수 있습니다.
정말 아름답습니다.
저 위의 복잡한 공식이 이렇게 간결하게 효율적으로 씌여질수 있다는게 놀라울 정도 입니다.

  • \(\lambda\) : 0 ~ 1 사이의 값
  • \(\delta_{t+l}\) : 해당 시점의 advantage function \(r_{t+l} + \gamma V(s_{t+l+1}) - V(s_{t+l})\) 입니다.
  • \(GAE(\gamma, 0)\) : \(A_t = \delta_t = r_t + \gamma V(s_{t+1}) - V(s_t)\)
  • \(GAE(\gamma, 1)\) : \(A_t = \sum^\infty_{j=0} \gamma^j r_{t+j} - V(s_t)\)

즉 \(\lambda\) 값을 0로 맞추면 1-step TD가 되고, 1로 맞추면 Monte Carlo가 되며,
이 두가지를 서로 섞었다고 볼 수 있습니다.