Youtube 영상 - {:.} REINFORCE 존시나 쉽게 설명 - {:.} 학습 완료된 후 플레이 영상 - {:.} 학습 중간 과정의 플레이 영상
Introduction - {:.} Value-based Algorithms - {:.} Policy-based Algorithms
Why Policy
Policy Gradient
REINFORCE Method - {:.} Algorithm - {:.} Value-based Learning 과 다른 점
Code - {:.} Model - {:.} Q-Function - {:.} Loss
Do not use REINFORCE becasuse.. - {:.} Full episodes are required - {:.} High gradients variance - {:.} Locally-Optimal Policy

Victor Freitas

Youtube 영상

REINFORCE 존시나 쉽게 설명

학습 완료된 후 플레이 영상

학습 중간 과정의 플레이 영상

Introduction

RL 방법론을 크게 두가지로 나뉘면 다음과 같습니다.

Value-based methods: 대표적으로 Q-Learning, Deep Q-Learning 등등이 있으며, value function에 의해서 각각의 state마다의 action에 대해서 가치(value)를 판단합니다. 즉 action과 value를 맵핑 시킨다고 보면 됩니다. 이를 통해서 현재 상태(state)에 대해서 가장 최적의 action을 찾을 수 있습니다. value-based methods는 action space가 한정적 discrete action일때 주로 사용합니다.
Policy-based methods: gradient of the policy를 찾는 REINFORCE 방식등이 있으며, 가치를 찾는게 아니라 policy를 다이렉트로 최적화 합니다. 이런 방식의 장점은 action space가 continuous이거나 stochastic일때 주로 사용을 합니다. 당연히 policy-based method에는 value function이 없습니다.

Value-based Algorithms

Q-Learning
Salsa
Value Iteration
DQN

Policy-based Algorithms

REINFORCE
Actor Critic
Crossentropy Method

Why Policy

Directly Finding Action

궁극적으로 RL의 최종 목표는 결론적으로 action을 잘 하는 것입니다.
예를 들어, 자율주행의 경우 운전을 잘하는 것이고, 게임의 경우 게임에서 승리하는 것이 보통의 목표입니다.
왜 굳이 state마다 정확한 가치를 알아야 하는지는 크게 중요하지 않습니다.

쉽게 말해 Value-based learning의 경우 각 state의 각각의 action마다 value를 구해서 action을 선택하는 것이 아니라
직접적으로 state -> action 으로 매핑을 한다는 의미 입니다.

argmax VS Softmax for Smooth Representation

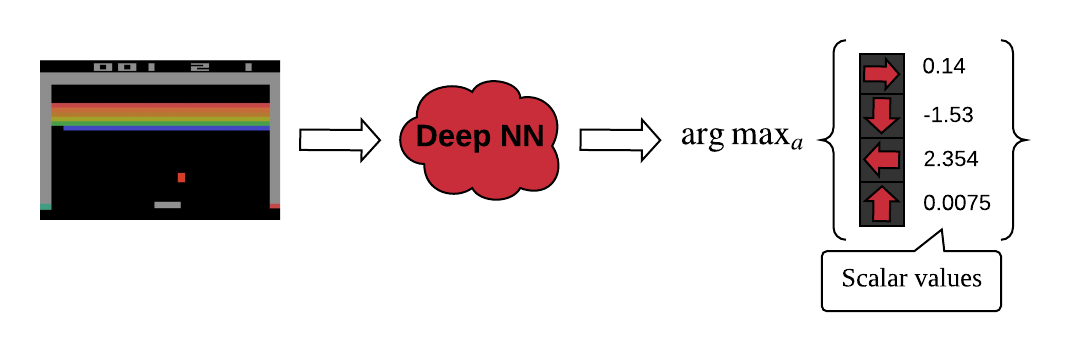
Value-based learning의 경우 output값이 scalar 값입니다.
그리고 보통의 policy-based learning의 경우 output값이 확률입니다. (일반적으로 softmax사용)

여기서 문제가 하나 생기는데.. 예를 들어서 DQN의 경우 output값이 scalar로서 value를 의미하기 때문에, output 값 자체가 널뛰기 하듯이 크게크게 변할수 있습니다. 예를 들어서 left action이 3.5의 가치를 나타낼때, gradient update를 하면서 5또는 1로 급격하게 변할수 있으며, 이는 학습에서 불안정성으로 이어질수 있습니다.

policy-based learning의 경우 확률값이기 때문에 gradient update를 하더라도 크게 변하지 않습니다.
예를 들어서 left action의 확률이 0.35 라고 할때, 업데이터 이후 0.36 또는 0.34 처럼 변합니다.
이는 다른 softmax를 사용해서 다른 actions들의 확률에 따라서 변하기 때문입니다.

Value-based Learning (DQN)

Policy-based Learning

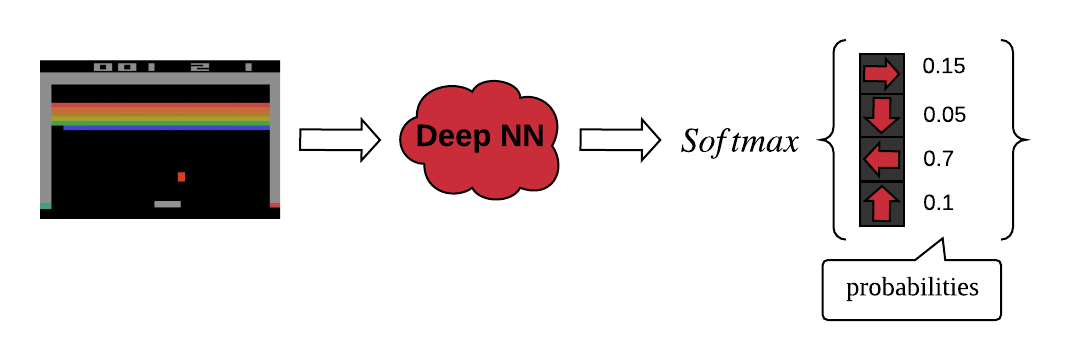
위의 그림에서 처럼 policy-based mehtod의 경우 softmax를 사용해서 확률로 사용을 하기 때문에 gradient가 업데이트 된다고 값이 크게 변하지 않습니다.

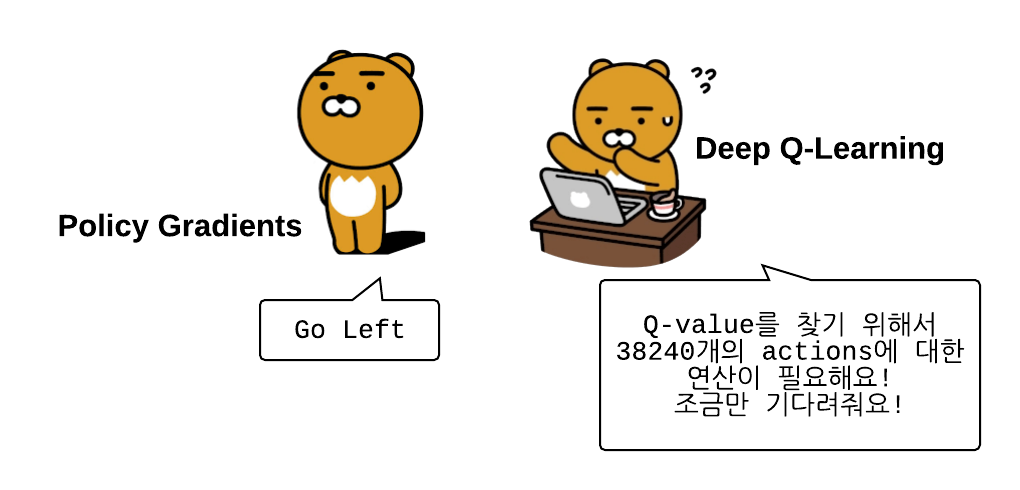
Continuous Action

Directly finding action과 사실 비슷한 말인데, continuous value같은 경우 각각의 모든 action들에 대한 q-value를 구하는 것은 어렵습니다. 예를 들어 0.0001 action에 대한 q-value 그리고 0.0002 에 대한 q-value 등등.. 사실.. 소수점자리로 가면 무한대로 q-value를 찾아야 합니다. (자동차 운전할때 몇도를 틀어야 되는지, 엑셀을 얼마만큼의 크기로 밟아야 하는지.. )

Policy-based learning의 경우 q-value찾는것 없이 바로 action을 찾기 때문에 매우 빠릅니다.

Policy Gradient

\[L = - Q(s, a) \log \pi(a | s)\]

\(Q(s, a)\): Accumulated total reward
- action에 대한 가치를 나타낸다
- scale of gradient
- 알고리즘에 따라 Q함수의 구현 방법은 각기 다르다
\(\log \pi(a \| s)\) : log-probability of the action taken
- gradient 값 자체로 봐도 됨

예를 들어서 둠 게임에서 left action을 했을때의 계산 방법은 다음과 같습니다.

즉 \(Q(s, a)\) 의 값이 큰데도 불구하고, \(\log \pi(a| s)\) 이 작을 경우..
이건 잘못된 행동이기 때문에.. \(L\) 의 값은 높아지며, NN가 업데이트 됩니다

앞에 negative (-) 마이너스 싸인이 있는 이유는 gradient descent를 하는 것이 아니라
gradient ascent를 함으로서 reward를 maximize시키기 때문입니다.

REINFORCE Method

위에서 정의한 PG 공식은 대부분의 policy-based methods에서 사용되는 방법이지만, 실제 구현은 알고리즘마다 다 다릅니다.
그 중의 하나가 REINFORCE Method방법입니다.

Cross-entropy method에서는 좋은 에피소드에는 \(Q(s, a) = 1\) 그리고 나쁜 에피소드에는 \(Q(s, a) = 0\) 을 주어서 학습을 시킵니다.
Cross-entropy method는 이렇게 간단한 가정에도 실제로 학습이 됩니다.
하지만 이렇게 단순하게 학습하는 것이 아니라 10점을 주거나 5점을 주거나 0점을 주거나 등등..
total reward에 따라서 주고자 한다면 REINFORCE Method를 사용하면 됩니다.

Algorithm

uniform probability distribution으로 NN를 초기화 함
N full episodes를 진행하고, \((s, a, r, s^\prime)\) transitions을 저장
episode k 의 step t 마다, 그 이후의 step에서 일어날 discounted total reward를 계산
\(Q_{k, t} = \sum_{i=0} \gamma^i r_i\)
모든 transitions에 대한 loss를 계산
\(L = - \sum_{k, t} Q_{k, t} \log \pi(s_{k, t}, a_{k, t})\)
SGD 업데이트를 실행하고 loss를 줄임
수렴할때까지 2번부터 계속 반복

Value-based Learning 과 다른 점

Q-Learning 같은경우 epsilon-greedy strategy를 사용해서 exploration을 했지만,
NN의 output이 확률값이며, 초기화는 uniform-distribution probability로 초기화 되었기 때문에 일종의 random behavior를 구현 할 수 있게 됩니다.

Replay memory를 사용하지 않음.
장단점이 있는데 PG의 경우 on-policy methods class에 속하며 쉽게 말하면 old policy에 의해서 축적된 데이터로는 학습을 할 수 없다는 뜻입니다.
여기에서의 장점은 converge가 비교적 빠르나, 단점은 environment와 더 많은 interaction을 요구하게 됩니다.

Code

Model

def create_model(input_size: int, n_actions: int, seed: int = 0):
    np.random.seed(seed)
    tf.set_random_seed(seed)

    model = Sequential()
    model.add(Dense(256, activation='relu', input_dim=input_size))
    model.add(Dropout(0.2))
    model.add(Dense(128, activation='relu'))
    model.add(Dropout(0.1))
    model.add(Dense(64, activation='relu'))
    model.add(Dense(n_actions, activation='softmax'))

    return model

Q-Function

def calculate_q_values(rewards: list, gamma: float):
    res = []
    sum_rewards = 0.0
    for r in rewards[::-1]:
        sum_rewards *= gamma
        sum_rewards += r
        res.append(sum_rewards)
    return list(reversed(res))

Loss

def _build_loss(self):
    action_probs = K.sum(onehot_actions * softmax_outputs, axis=1)
    score = - discouted_rewards * K.log(action_probs)
    score = K.mean(score)

Do not use REINFORCE becasuse..

Full episodes are required

Cartpole을 실제 구현해보면 알겠지만.. 학습을 하면 할 수록 점점 학습시간이 늘어나게 됩니다.
이유는 한번의 gradient 값을 알기 위해서는 N번의 게임을 처음부터 끝까지 다 하고 최종 score로 gradient값을 찾기 때문입니다.
학습을 시키면 시킬수록 봉을 계속 서있게 만드는 시간이 기하급수적으로 늘어나게 되며.. 학습또한 언제 끝날지 모를 정도로 느립니다.

DQN에서 확인했듯이, REINFORCE처럼 아주 정확한 discounted reward를 찾을 필요 없이, one-step Bellman equation만 있어도 학습은 가능합니다.

\[Q(s, a) = r_a + \gamma V(s^\prime)\]

하지만 REINFORCE에서는 그냥 정확한 accumulated total reward가 필요합니다.

High gradients variance

PG공식을 보면.. gradient값은 사실상 환경에 따라 크게 달라질수 있습니다.
예를 들어서 left action에 대한 q-value가 1점이 될수도 있고, 5599점이 될 수도 있습니다.

또한 누적이기 때문에 Cartpole의 경우 5 steps동안 pole을 들었다면 5점을 받지만,
학습이 되서 10000steps동안 들고 있다면 10000점이나 됩니다.
즉 gradient의 값은 5에서 10000점까지 지나치게 크게 변할 수 있으며,
학습에서 아주 몇개의 지나치게 크게 받은 gradient값이 나머지 게임에서 얻은 작은 gradient를 모두 압도해버리거나..
지나치게 크게 업데이트가 되서 미세하게 gradient 업데이터가 안될수도 있다는 뜻이 됩니다.

해결 방법은.. reward의 평균값으로 빼주거나 log를 씌워주거나.. 등등..
목표는 었쟀든 너무 지나치게 크지 않도록 변형해 줍니다.

Locally-Optimal Policy

DQN에서는 exploration을 위해서 epsilon-greedy acction selection을 사용해서 local minima에 빠지지 않도록 했습니다.
PG에서는 확률을 사용하지만 매우 높은 확률로 local minima에 빠질 가능성이 있습니다.

Exploration을 잘하기 위해서 policy에 대한 entropy를 구해서 이를 loss에 사용하는 방법이 있습니다.

Entropy는 information theory에서 불확실성을 나타냅니다.
즉.. 어떤 action을 취할지 아직 잘 모르겠다면.. (불확실성이 높은 상태이라면..) 지나치게 특정 action을 취하지 않도록 막을 수 있습니다.

\[H(\pi) = - \sum \pi(a|s) \log \pi(a|s)\]

예를 들어서 다음과 같을 수 있습니다.

\[\begin{align} H(\pi) &= 1.08 & \pi(a|s) = [0.3, 0.3, 0.3] \\ H(\pi) &= 0.102 & \pi(a|s) = [0.01, 0.01, 0.99] \end{align}\]

이렇게 나온 entropy값을 loss에 빼줘서 불확실성이 높을때는 gradient값도 높지 않도록 만듭니다.

\[L - H(\pi)\]