Switch Transformer - Scaling to Trillion Parameter Models with Simple and Efficient Sparsity
- Switch Transformer - Scaling to Trillion Parameter Models with Simple and Efficient Sparsity
- Problem
- Model
- Switch Transformer
- Implementation
Switch Transformer - Scaling to Trillion Parameter Models with Simple and Efficient Sparsity
| Key | Value |
|---|---|
| Paper | https://arxiv.org/pdf/2101.03961 |
| publication Date | 2021 |
Problem
MoE (Mixture of Experts) 모델은 inputs 마다 서로다른 parameters 사용하기 때문에, 전체 parameters 수는 폭발적으로 늘어나도, 실제 사용하는 부분은 소수라 연산량은 일정합니다.
하지만 실제 적용은 어렵습니다.
- 기존 MoE 모델의 문제점
- 복잡한 Routing 알고리즘이 필요
- communication overhead가 큼
- 학습 불안정성 gradient exploding 현상 발생
- Switch Transformer 는 이러한 기존의 문제들을 해결하였음.
Model
핵심은
- Sparse Training
- 궁극적으로 parameter 갯수 자체를 maximize 하는 것. (매우 효율적인 방식으로)
- 이렇게 parameters 를 늘리지만, Floating point operations (FLOPs) 를 constant 값으로 바꾸는 것.
- 즉 parameters 는 늘리지만, 연산은 constant 하게 됨.
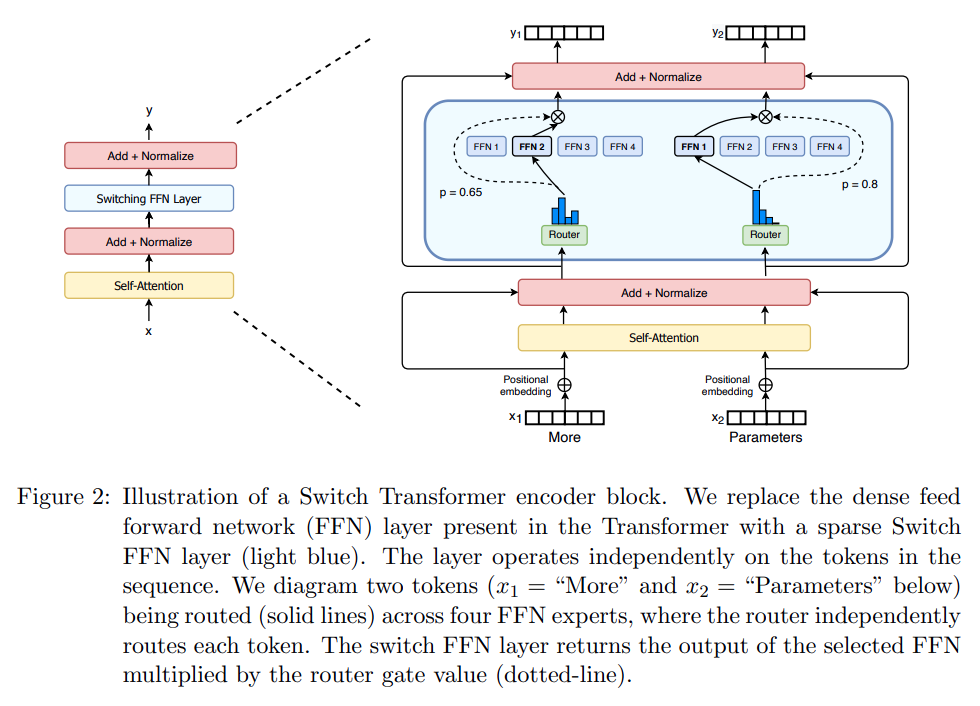
기존 MOE 모델 방식 - Mixture of Experts Routing
- MOE (Mixture of Experts) 개념은 이미 2017년 Shazeer et al에 의해 제안되었음.
- route 에 해당하는 \(W_r\) 값이 존재하고, input값과 곱해져서 logits을 생성함 \(h(x) = W_r \cdot x\)
- 이후에 softmax를 적용하고, top-k 개의 experts 를 선택함. 포인트는 여러개의 experts를 선택함
아래는 구체적인 공식
\[h(x) = W_r \cdot x\]- W_r : route matrix (이게 학습이 되면서 experts를 선택하는 역활을 함)
- x: input vector
이후에 softmax를 적용하여, top-k개의 experts를 선택함.
\[p_i(x) = \frac{e^{h(x)_i}}{\sum^N_j e^{h(x)_j}}\]만약 T가 선택된 experts의 집합이라면, 최종 output은 다음과 같이 계산됩니다.
\[y = \sum_{i \in T} p_i(x) E_i(x)\]- E_i(x): 선택된 experts에서 i번째 expert의 output
- 그냥 곱하기 하면 됨
이걸 Pytorch 로 구현하면 다음과 같습니다.
import torch
import torch.nn as nn
import torch.nn.functional as F
class MoELayer(nn.Module):
def __init__(self, input_dim, output_dim, num_experts=4, k=2):
super().__init__()
self.k = k
self.num_experts = num_experts
# Router: logits = W_r · x
self.router = nn.Linear(input_dim, num_experts)
# Experts: each is a small MLP (or Linear here)
self.experts = nn.ModuleList([
nn.Linear(input_dim, output_dim) for _ in range(num_experts)
])
def forward(self, x):
"""
x: (batch_size, input_dim)
returns: (batch_size, output_dim)
"""
# Compute routing logits
logits = self.router(x) # (B, N)
gate_probs = F.softmax(logits, dim=-1) # (B, N)
# Select top-k experts per example
topk_vals, topk_idx = torch.topk(gate_probs, self.k, dim=-1) # (B, k)
# Initialize output
output = torch.zeros(x.size(0), self.experts[0].out_features, device=x.device)
for i in range(self.k):
idx = topk_idx[:, i] # expert index
weight = topk_vals[:, i].unsqueeze(1) # (B, 1)
# For batch-wise selection
expert_outputs = torch.stack([
self.experts[expert_id](x[j].unsqueeze(0))
for j, expert_id in enumerate(idx)
]).squeeze(1) # (B, output_dim)
output += weight * expert_outputs # weighted sum
return output
The problem of MOE Routing
2017년도에 나온 Mixture of Experts의 모델은 복잡한 routing알고리즘이 필요했습니다. 특히 1개 이상의 expersts를 선택하는 방식을 취했는데, 그 이유는 non-trivial gradients 를 갖기 때문이라고 합니다.
- trivial gradients: gradients 값이 0에 가까운 매우 작은 수 -> 학습이 안됨
- non-trivial gradients: 실제로 의미있는 (학습이 가능한) gradients
만약 softmax 의 결과값 중에서 하나만 취하게 된다면, argmax 를 사용할수 있습니다.
idx = torch.argmax(logits)
문제는 argmax를 사용하게 되면 non-differentiable 연산이기 때문에, backpropagation이 불가능하게 됩니다.
(그냥 큰 값을 선택해서 index를 리턴하는 것기 때문에 discrete operation 이며, discontinuous function임 -> 미분 안됨)
즉 해당 값이 왜 선택되었는지, gradient 정보가 없습니다.
따라서 여러개를 선택하는 방식이 필요했습니다.
Expert Capacity
Switch Transformer 를 배우기 전에, 먼저 Expert Capacity 개념을 이해해야 합니다.
- Imbalance는 expert 가 선택되는 빈도에 따라서 발생하기도 합니다.
예를 들어서 “Mixture of Experts is AWESOME” 이라는 문장이 Router를 거쳤을때, 특정 Expert 만 선택된다면 undertraining이 발생할수 있습니다.
Token Softmax(logits) Selected Expert
------------------------------------------------------------
Mixture [0.7, 0.1, 0.1, 0.1] Expert 0
of [0.8, 0.1, 0.0, 0.1] Expert 0
Experts [0.6, 0.1, 0.1, 0.2] Expert 0
is [0.5, 0.2, 0.1, 0.2] Expert 0
AWESOME [0.1, 0.1, 0.7, 0.1] Expert 2
즉 어떤 expert가 선택 되느냐가 아니라, 얼마나 많이 특정 expert가 선택되느냐가 중요합니다.
해당 문제를 해결하기 위해서, Expert Capacity 개념이 도입되었습니다.
특정 expert의 capacity (token의 갯수)를 정해놓고, 해당 capacity를 초과하는 경우에는 다른 expert를 선택하도록 합니다.
이것을 “token overflow” 라고 합니다.
Transformer 모델 쓰는데, 어떻게 이게 가능하냐 라고 생각이 들면 아키텍쳐를 보면 이해가 됩니다.
Input Sentence (문장)
↓
Tokenization
↓
Embedding
↓
Multi-Head Attention (공통 처리)
↓
FFN (token마다 expert 선택!)
↓
Output
즉 FFN 부분에서 expert가 선택되고 FFN가 처리되기 때문에, token마다 다른 expert가 선택될 수 있습니다.
그래서 expert capacity를 정해놓고, 해당 capacity를 초과하는 경우에는 다른 expert를 선택하도록 정할수 있습니다.
또는 dropped token 이라고 해서, 해당 token을 처리하지 않고, 넘어가도록 할수도 있습니다.
- tokens_per_batch: 배치당 토큰의 갯수
- num_experts: 전체 expert의 갯수
- capacity_factor: expert의 capacity를 조정하는 factor (예를 들어서 1.0 이면, 각 expert가 배치당 토큰의 갯수 / 전체 expert의 갯수 만큼의 capacity를 갖게 됨)
예제
\[\text{Expert Capacity} = \left( \frac{100}{4} \times 1.0 \right) = 25\]각 Expert는 배치당 25개의 토큰을 처리할 수 있습니다.
만약 어떤 expert가 25개를 초과하는 경우에는 다른 expert를 선택하거나, dropped token 으로 그냥 스킵합니다.
보통 capacity_factor는 1.0 에서 1.5 사이로 설정합니다.
- capacity_factor 가 높을수록: dropped token이 줄어듬 -> 반면에 연산량이 늘어남
- capacity_factor 가 낮을수록: dropped token이 늘어남 -> 반면에 연산량이 줄어듬
아래는 Switch Transformer 사용시 capacity factor가 줄어들면서 , 연산량이 줄어드는 것을 보여줍니다.
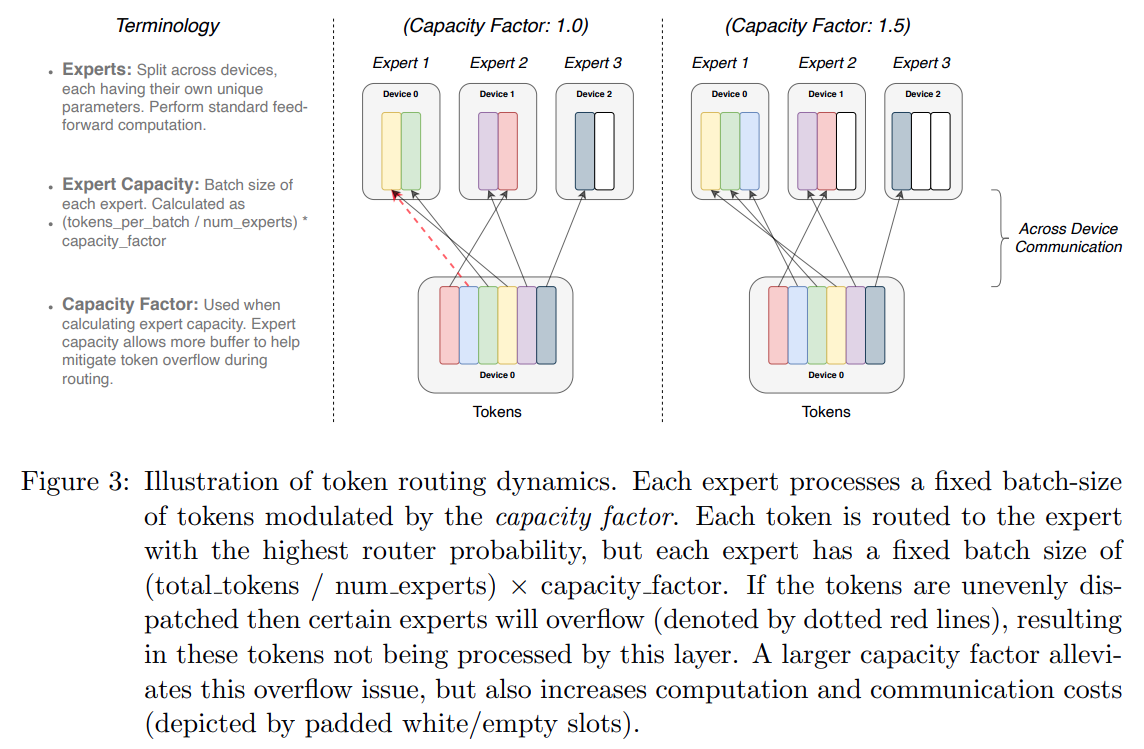
Switch Transformer
Switch Routing: Rethinking Mixture of Experts
Switch Transformer 는 이러한 복잡한 Routing 알고리즘을 단순화 하면서, 더 높은 성능을 보여줍니다.
즉 k=1 routing은 Switch Routing이라고 부릅니다.
이로인 인한 장점은 다음과 같습니다.
- Router computation 이 단순해지며, 오직 single expert만 선택합니다.
- expert capacity가 반으로 줄어들수 있습니다.
- routing implementaion이 단순해집니다.
1번은 single expert만 선택하기 때문에, routing computation이 단순해집니다.
2번은 expert capacity에서 쉽게 말하면, dropped token이 발생하면서 연산량이 줄어들수 있습니다.
3번은 그냥 구현이 단순해집니다.
Differentiable Load Balancing Loss
\[\begin{align} P_i &= \frac{1}{T} \sum_{x \in \beta} p_i(x) \\ fi &= \frac{1}{T} \sum_{x \in \beta} \mathbf{1} \{ argmax p(x) = i \} \\ loss &= \alpha \cdot N \cdot \sum^N_{i=1} f_i \cdot P_i \\ \end{align}\]- P_i
- \(P_i (X)\): token x가 expert i로 갈 확률. (softmax의 결과값)
- f_i
- T: batch안의 token 갯수
- argmax p(x): token x를 라우팅할때 선택된 expert의 index
- 쉽게 설명하면, batch 안의 token이 expert i로 라우팅 됐는지 비율
- 예를 들어서 batch안에 token이 100개가 있고, 그중에 20개가 expert i로 라우팅 됐다면, f_i = 0.2 가 됩니다.
- loss
- a (alpha): scaling factor (hyperparameter 이며 보통 0.01로 설정)
- N: number of experts
- f_i: 실제 routing된 token 중에서 expert i에 할당된 비율 (fraction of tokens dispatched to expert i)
- P_i: expert i에 할당된 확률 총합 (평균)
즉, 실제 token 분배 분포 f_i 와 router (softmax)의 분포 P_i 의 dot product를 계산 -> scaling 계수를 곱한것
f_i (token 분배 분포) 와 P_i (softmax의 분포)가 일치할수록 loss가 작아집니다.
(이때 gradient계산 할때 f 는 non-differentiable 이며, P는 differentiaible 입니다.)
즉 다음은 “완벽히 균형 잡힌 상태 (ideal case)” 입니다.
Expert: E1 E2 E3 E4
f_i: 0.25 0.25 0.25 0.25 (실제 라우팅 분포)
P_i: 0.25 0.25 0.25 0.25 (softmax 기대 확률)
f_i * P_i: 0.0625 0.0625 0.0625 0.0625
Sum(f ⋅ P): 0.25 (최소값!)
만약 편향된 상태가 된다면, 다음과 같습니다.
Expert: E1 E2 E3 E4
f_i: 0.70 0.10 0.10 0.10 (거의 E1만 쓰임)
P_i: 0.40 0.20 0.20 0.20 (softmax도 약간 E1 치우침)
f_i * P_i: 0.28 0.02 0.02 0.02
Sum(f ⋅ P): 0.34 (커짐 → loss ↑)
Router Implementation
import torch
import torch.nn.functional as F
from torch import nn
class Router(nn.Module):
"""
The router module determines which expert each token is sent to.
It also computes the load balancing loss.
"""
def __init__(self, d_model, num_experts):
super().__init__()
self.num_experts = num_experts
self.gate = nn.Linear(d_model, num_experts)
def forward(self, x):
# x: (batch_size, seq_len, d_model)
logits = self.gate(x)
# logits: (batch_size, seq_len, num_experts)
# Get the top-1 expert for each token
top1_logits, top1_indices = logits.max(dim=-1)
# top1_indices: (batch_size, seq_len)
# Create a one-hot encoding of the expert indices
# This will be used to dispatch tokens to the correct expert
expert_mask = F.one_hot(top1_indices, self.num_experts).float()
# expert_mask: (batch_size, seq_len, num_experts)
# Calculate the load balancing loss
# This loss encourages all experts to be used equally.
# Count how many tokens are sent to each expert
tokens_per_expert = expert_mask.sum(dim=(0, 1)) # (num_experts)
# Total number of tokens
total_tokens = x.size(0) * x.size(1)
# Calculate the fraction of tokens sent to each expert
fraction_tokens_per_expert = tokens_per_expert / total_tokens
# Calculate the expert probabilities from the logits
expert_probs = F.softmax(logits, dim=-1).mean(dim=(0, 1)) # (num_experts)
# The load balancing loss is the dot product of these two quantities
load_balancing_loss = self.num_experts * torch.dot(fraction_tokens_per_expert, expert_probs)
return expert_mask, load_balancing_loss
Expert Capacity
Implementation
여기서 전체 코드가 아닌 핵심이 되는 코드만 공유 합니다.
Switch Transformer Model
Input Tokens
│
▼
[Embedding Layer] ──► nn.Embedding(ntoken, d_model)
│
▼
[Positional Encoding] ──► PositionalEncoding(d_model, dropout)
│
▼
[Transformer Encoder Stack]
│
└─► (L layers of)
└─► [Multi-head Attention]
└─► [LayerNorm + Residual]
└─► [Switch FFN (MoE Layer)]
└─► Router → Expert selection
└─► Dispatch token to Expert
└─► Gather output
└─► [LayerNorm + Residual]
│
▼
[Final Linear Decoder] ──► nn.Linear(d_model, ntoken)
│
▼
Vocabulary Logits (for language modeling)
class SwitchTransformerLM(nn.Module):
def __init__(self, ntoken: int, d_model: int, nhead: int, d_ff: int, num_experts: int, num_layers: int,
dropout: float = 0.5):
super().__init__()
self.model_type = 'Transformer'
self.d_model = d_model
self.encoder = nn.Embedding(ntoken, d_model)
self.pos_encoder = PositionalEncoding(d_model, dropout)
encoder_layer = SwitchTransformerEncoderLayer(d_model, nhead, d_ff, num_experts, dropout)
self.transformer_encoder = SwitchTransformerEncoder(encoder_layer, num_layers)
self.decoder = nn.Linear(d_model, ntoken)
SwitchTransformer Encoder Layer + MoE Layer
Input: Token Hidden States (src)
│
▼
[Multi-Head Self-Attention]
│
▼
🟦 MoELayer ← ← ← ← ← ← ← ← ← ← ← ← ← 🧠 핵심 포인트!
│
├─► Router(x)
│ └─► Routing logits (W_r · x)
│ └─► Softmax → Top-1 Expert 선택
│ └─► expert_mask 생성 (one-hot)
│
├─► Capacity 계산 (token overflow 방지)
│
├─► 각 Expert 별로:
│ └─ Token dispatch (x[expert_indices])
│ └─ Expert FFN 처리
│ └─ Output scatter to original positions
│
└─► 최종 Output (sparse computation 결과)
+ Load Balancing Loss
▼
Dropout + Residual
▼
LayerNorm #2
▼
Output Hidden States, Load Balancing Loss
SwitchTransformerEncoderLayer 에서 가장 중요한 부분은 아래 코드이며,
기존 TransformerEncoderLayer와 MoELayer를 결합한 것입니다.
Attention 연산 후에 MoE layer를 적용하여, 각 토큰마다 다른 expert를 선택하고 처리합니다.
class SwitchTransformerEncoderLayer(nn.Module):
def __init__(self, d_model: int, nhead: int, d_ff: int, num_experts: int, dropout: float = 0.1) -> None:
super().__init__()
self.self_attn = nn.MultiheadAttention(d_model, nhead, dropout=dropout)
self.moe_layer = MoELayer(d_model, d_ff, num_experts)
self.norm1 = nn.LayerNorm(d_model)
self.norm2 = nn.LayerNorm(d_model)
self.dropout = nn.Dropout(dropout)
def forward(self, src: Tensor,
src_mask: Optional[Tensor] = None,
src_key_padding_mask: Optional[Tensor] = None) -> Tuple[Tensor, Tensor]:
# Multi-head self-attention
src2 = self.self_attn(src, src, src, attn_mask=src_mask, key_padding_mask=src_key_padding_mask)[0]
src = src + self.dropout(src2)
src = self.norm1(src)
# MoE layer
src2, load_balancing_loss = self.moe_layer(src)
src = src + self.dropout(src2)
src = self.norm2(src)
return src, load_balancing_loss
MoE Layer
Input (x): (batch_size, seq_len, d_model)
│
▼
Router (W_r · x → softmax → top-1 expert 선택)
│
▼
Expert Mask (one-hot): (batch_size, seq_len, num_experts)
│
▼
Flatten: x → (B×T, d_model), mask → (B×T, num_experts)
│
▼
for each expert i in num_experts:
- token 선택 (해당 expert로 라우팅된 것만)
- capacity 초과 시 overflow drop
- expert_i(input) → FFN 처리
- 결과를 final_output 에 다시 index_add
▼
Reshape: (B×T, d_model) → (batch_size, seq_len, d_model)
Return: final_output, load_balancing_loss
class MoELayer(nn.Module):
"""
The Mixture-of-Experts (MoE) layer, which replaces the FFN layer in a standard Transformer.
"""
def __init__(self, d_model: int, d_ff: int, num_experts: int, capacity_factor: float = 1.25) -> None:
super().__init__()
self.d_model = d_model
self.num_experts = num_experts
self.capacity_factor = capacity_factor
self.router = Router(d_model, num_experts)
self.experts = nn.ModuleList([Expert(d_model, d_ff) for _ in range(num_experts)])
def forward(self, x: Tensor) -> Tuple[Tensor, Tensor]:
"""
Example: Let's say we have:
- batch_size=2, seq_len=4, d_model=8, num_experts=2
- Input x: shape (2, 4, 8) - 2 sequences, each with 4 tokens of 8 dimensions
"""
# x: (batch_size, seq_len, d_model)
# Example: x.shape = (2, 4, 8)
batch_size, seq_len, d_model = x.shape
# Get the expert mask and load balancing loss from the router
# The router decides which expert should process each token
expert_mask, load_balancing_loss = self.router(x)
# expert_mask: (batch_size, seq_len, num_experts)
# Example: expert_mask.shape = (2, 4, 2)
# expert_mask[0, 0, :] = [1, 0] means token 0 goes to expert 0
# expert_mask[0, 1, :] = [0, 1] means token 1 goes to expert 1
# Determine the capacity of each expert
capacity = int((seq_len / self.num_experts) * self.capacity_factor)
# Reshape tensors for easier processing - flatten batch and sequence dimensions
x_flat = x.view(-1, d_model) # (batch_size * seq_len, d_model)
expert_mask_flat = expert_mask.view(-1, self.num_experts) # (batch_size * seq_len, num_experts)
# Initialize output tensor with zeros - same shape as flattened input
final_output = torch.zeros_like(x_flat)
# Example: final_output.shape = (8, 8)
# Process each expert separately
for i, expert in enumerate(self.experts):
# Find which tokens should go to this expert (non-zero entries in the mask)
expert_indices = torch.where(expert_mask_flat[:, i] > 0)[0]
# Example for expert 0: expert_indices might be [0, 2, 4] (tokens 0, 2, 4)
# Example for expert 1: expert_indices might be [1, 3, 5, 6, 7] (tokens 1, 3, 5, 6, 7)
# Apply capacity constraint - if too many tokens assigned, keep only the first 'capacity' tokens
if expert_indices.shape[0] > capacity:
expert_indices = expert_indices[:capacity]
# Example: if expert 1 has 5 tokens but capacity=2, keep only [1, 3]
# Process tokens assigned to this expert
if expert_indices.shape[0] > 0:
# Extract the tokens that should go to this expert
expert_input = x_flat[expert_indices]
# Example: if expert_indices=[1, 3], expert_input.shape = (2, 8)
# Process the tokens through the expert network
expert_output = expert(expert_input)
# Example: expert_output.shape = (2, 8) - same as expert_input
# Ensure dtype consistency
expert_output = expert_output.to(final_output.dtype)
# Place the expert's output back to the final output at the correct positions
# Switch Transformer uses exclusive routing: each token goes to exactly ONE expert
# So we use assignment (=) not addition (+=)
# Example: if expert_indices=[1, 3] and expert_output has 2 rows
# final_output[1] = expert_output[0] # Place expert's output for token 1
# final_output[3] = expert_output[1] # Place expert's output for token 3
for j, token_idx in enumerate(expert_indices):
final_output[token_idx] = expert_output[j]
# Reshape back to original dimensions
final_output = final_output.view(batch_size, seq_len, d_model)
# Example: final_output.shape = (2, 4, 8) - back to original shape
return final_output, load_balancing_loss