SimCSE - Simple Constrastive Learning of Sentence Embeddings
- SimCSE - Simple Constrastive Learning of Sentence Embeddings
- Problem
- Summary of the Model
- Detailed Explanation
SimCSE - Simple Constrastive Learning of Sentence Embeddings
| Key | Value |
|---|---|
| Paper | https://arxiv.org/abs/2104.08821 |
| publication Date | 2021 |
Problem
- 기존 방식
- 기존 문방 embedding 방식은 문장간 의미적 유사도를 잘 반영하지 못했음
- 따라서 기존 방식은 data augmentation또는 복잡한 학습 전략 없이는 성능 한계가 있었음
- supervised 방식은 많은 labeled data가 필요했음
- SimCSE
- SimCSE는 Dropout만 간단하게 사용해, data augmentation을 수행함
- constrastive learning을 통해서 문제를 해결
Summary of the Model
- Unsupervised and Supervised (두가지 방식 모두 지원)
- Unsupervised SimCSE
- 단순히 input sentence 자신을 dropout한 이후에 자기 자신을 예측 하는 방식
- 즉 동일한 문장을 pretrained model에 “두번” 넣은후 -> dropout -> 두개의 문장 embedding을 얻음
- 이렇게 얻은 두개의 embeddings은 positive pairs 로 간주됨
- 이후 동일한 mini batch내에서 다른 문장들은 “negatives” 로 간주함
- representation collapse에 강함
- 서로 다른 다양한 문장들이 동일한 embedding으로 수렴되는 현상
- Dimensional Collapse: embedding vectors들이 전체 embedding space가 아니라 특정한 저차원 공간에 “집중”되는 현상
- Representation Collapse: Vector Quantization 에서 주로 발생하는 현상으로, 특정한 클러스터 대표값으로 묶이면서, 다양한 패턴을 잃어버리는 현상
- Neural Collapse: 분류 문제에서, embeddings들이 같은 클래스의 대표값 (평균값)으로 수렴하는 현상
- 단순히 input sentence 자신을 dropout한 이후에 자기 자신을 예측 하는 방식
- Supervised SimCSE
- NLI 데이터셋을 사용
- 기존 3-way classification (entailment, neutral, contradiction) 사용 대신에, entrailment pairs 를 positive pairs로 사용하였음
- 추가적으로 contradiction paris를 hard negative 로 사용했을때 성능이 더 향상되었음
- NLI 데이터셋을 사용
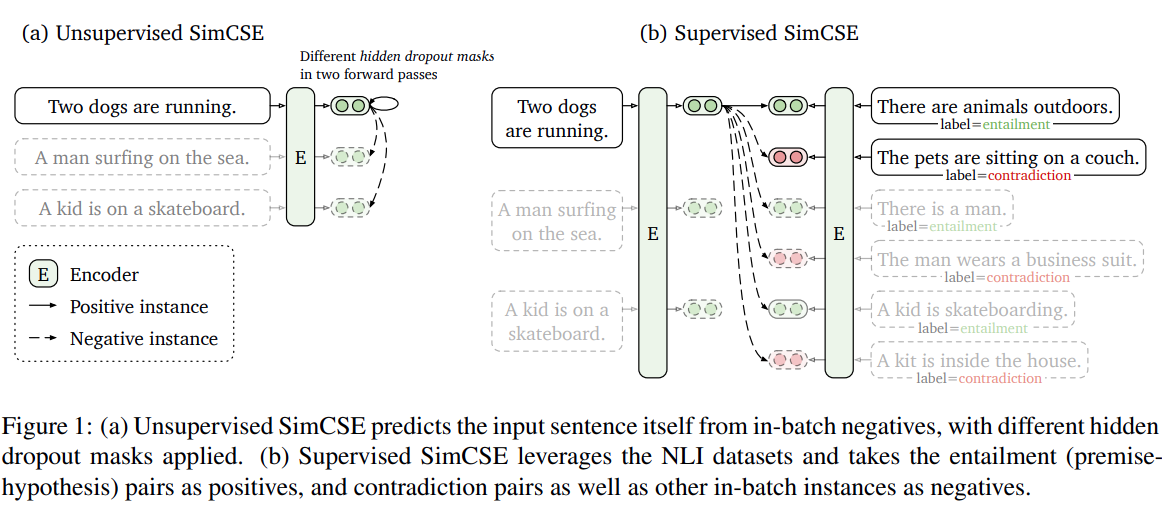
Detailed Explanation
Unsupervised SimCSE
Unsupervised SimCSE는 label 없이도 문장 표현 학습이 가능한 방식으로, 아주 간단하면서도 효과적인 전략을 사용합니다.
방식은 다음과 같습니다
동일한 문장을 dropout을 두번 적용하여 embedidngs 을 생성 -> 이 둘을 positive pair로 간주하여 constrastive learning을 수행
1. 입력 문장 s
↓
2. 같은 sentence → encoder 통과 (dropout 적용)
↓
┌──────────────┐ ┌──────────────┐
│ z1 = BERT(s)│ │ z2 = BERT(s)│
│ (1st dropout)│ │ (2nd dropout)│
└──────────────┘ └──────────────┘
↓ ↓
Positive Pair: (z1, z2) ←──────┐
│
│
Same sentence with different noise
│
↓ ↓
3. 다른 문장들의 embedding은 모두 negative로 간주
↓
4. InfoNCE loss로 contrastive 학습 수행
이렇게 하는 이유는 예를 들어 image라면 crop, flip, rotation, distortion등으로 augmentation을 수행할 수 있지만,
문장에서는 dropout이 가장 간단하면서도 효과적인 방법이기 때문입니다.
- 동일한 문장을 두 번 인코딩하면 dropout 때문에 서로 조금씩 다른 embedding이 나옴
- 이 두 벡터가 positive pair가 되고,
- 같은 배치에 있는 다른 문장 embedding들은 전부 negative pair로 간주
- 이렇게 batch 내부에서만 positive/negative를 구성하여 학습
Constrastive Learning
\[L = -log \frac{e^{sim(h_i, h^+_i) / \tau }}{ \sum^N_{j=1} e^{sim(h_i, h_j) / \tau}}\]- \(h_i, h^+_i\) : positive pair (dropout으로 생성된 두개의 문장 embedding)
- \(sim(...)\) : cosine similarity \(\frac{h_i \cdot h^+_i}{\|h_i\| \cdot \|h^+_i\|}\)
- \(\tau\) : temperature hyperparameter 보통 0~1 사이의 값이며 보통 0.05로 설정
- 낮은값 (0.05): 빠른 수렴이지만, 오버피팅 위험 가능성
- 높은값 (0.1): 느린 수렴이지만, 더 일반화된 표현을 학습할 수 있음
cosine similarity 계산하는 부분
- F.normalize(z1, dim=-1) 는 벡터를 L2 norm으로 정규화 합니다. \(\frac{z_i}{ \| z_i \|_2}\)
- z / torch.sqrt(z**2).sum()) 이것과 동일한 의미입니다.
- L2 norm으로 정규화된 벡터는 서로 dot product (내적)을 계산하면, cosine similarity가 됩니다.
label 생성하는 부분
- z1: 문장 A, B, C, D → [z1[0], z1[1], z1[2], z1[3]]
- z2: 위 문장 A, B, C, D 를 dropout해서 다시 만든 버전 → [z2[0], z2[1], z2[2], z2[3]]
각 anchor embedding (row)에 대해
이 anchor의 정답 positive가 z의 몇 번째 위치에 있는지를 알려주는 label 배열을 만들기
쉽게 말하면, 서로의 index를 맞추는 작업.
def simcse_loss(self, z1, z2):
"""
Compute SimCSE loss using InfoNCE
Args:
z1: [batch_size, hidden_size] - first representations
z2: [batch_size, hidden_size] - second representations (dropout augmented)
Returns:
loss: contrastive loss
"""
# Normalize embeddings
z1 = F.normalize(z1, dim=-1)
z2 = F.normalize(z2, dim=-1)
# Concatenate z1 and z2
z = torch.cat([z1, z2], dim=0) # [2*batch_size, hidden_size]
# Compute similarity matrix (matmul is dot product)
sim_matrix = torch.matmul(z, z.t()) / self.temp # [2*batch_size, 2*batch_size]
batch_size = z1.size(0)
# Create labels for positive pairs
# For i-th sample in z1, its positive is (i+batch_size)-th sample in z2
# For i-th sample in z2, its positive is (i-batch_size)-th sample in z1
# labels = [4, 5, 6, 7, 0, 1, 2, 3] for batch_size=4
labels = torch.arange(2 * batch_size, device=z.device)
labels[:batch_size] += batch_size # z1's positives are in z2
labels[batch_size:] -= batch_size # z2's positives are in z1
# Mask out diagonal (self-similarity)
# We don't want to compare a sample with itself
# tensor([[ -inf, 0.0000, 0.9939, 0.1104],
# [0.0000, -inf, 0.1104, 0.9939],
# [0.9939, 0.1104, -inf, 0.2195],
# [0.1104, 0.9939, 0.2195, -inf]])
mask = torch.eye(2 * batch_size, device=z.device).bool()
sim_matrix = sim_matrix.masked_fill(mask, -float('inf'))
# Compute cross-entropy loss
loss = F.cross_entropy(sim_matrix, labels)
return loss