Introduction

해당 문서는 아래의 내용을 정리/구현 하였습니다.

  1. Pytorch Tutorial - TRANSLATION WITH A SEQUENCE TO SEQUENCE NETWORK AND ATTENTION
  2. Paper - Sequence to Sequence Learning with Neural Networks

Seq2Seq가 나오기 전의 DNN의 문제는 input 그리고 output의 length가 fixed dimensionality로 제한되는 문제를 갖고 있습니다.
특히 speech recognition, machine translation 그리고 question answering문제 모두
input 그리고 output의 sequence length가 서로 다르며, 미리 고정시킬수 없는 문제를 갖고 있습니다.

예를 들어서 “Where will you go this evening?” 은 모두 6글자로 이루어져 있으며,
일본어로 변환시 “今晩どこに行きますか？” 총 10글자로 이루어집니다. (일본어는 구글 번역기로 돌렸는데 일본어가 맞는지 모르겠네요)
즉 단순 LSTM, RNN계열로 문제를 다룰시, input의 sequence length에 따라서 output도 정해지는 문제가 있으며, 이를 해결해야 합니다.

2014년 구글 논문에서 Seq2Seq 모델에 Attention을 더해서 이러한 문제들을 해결했습니다.

Sequence to Sequence Model

Seq2Seq Model

Seq2Seq은 2개의 RNN구조로 이루어져 있으며, 중간에 intermediate vector가 존재합니다.

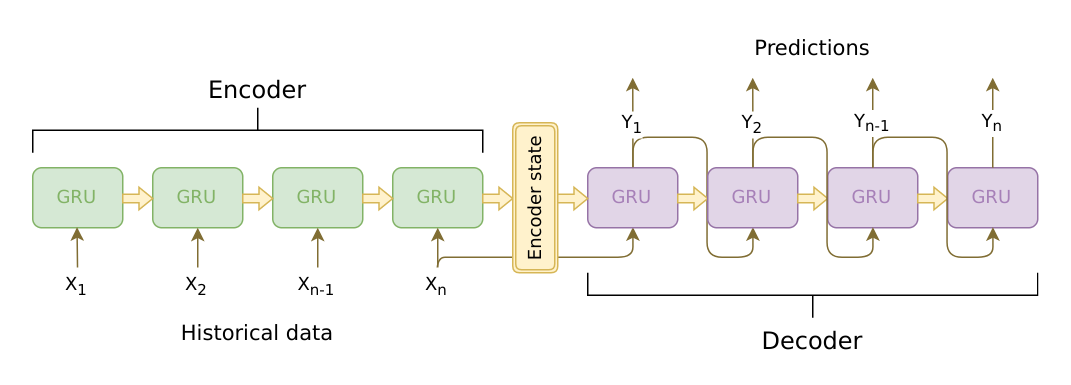
image source:https://jeddy92.github.io/JEddy92.github.io/ts_seq2seq_intro/
  • 아래에 (skippable) 이 있으면 그냥 넘어가도 됩니다. 그림만 이해되면 되고, 똑같은 말을 수학으로 적어놓은 것 뿐입니다.

Input and Output (skippable)

  • \(\mathcal{V}^{(I)}\) : Input의 모든 단어
  • \(\mathcal{V}^{(O)}\) : Output의 모든 단어
  • \(\mathbf{X}\) : Input
  • \(\mathbf{Y}\) : Output
  • \(\mathbf{x}_i\) : i-th element of the Input (즉 i 번째의 one-hot vector의 input 단어) (따라서 \(\mathbf{x}_i \in \mathcal{V}^{(I)}\) 를 만족합니다)
  • \(\mathbf{y}_j\) : j-th element of the Output (즉 j 번째의 one-hot vector의 output 단어) (따라서 \(\mathbf{y}_j \in \mathcal{V}^{(O)}\) 를 만족합니다)
  • \(I\) : the length of the input sequence
  • \(J\) : the length of the output sequence
  • \(\mathbf{y}_0\) : one-hot vector of BOS (beginning of the sentence)
  • \(\mathbf{y}_{j+1}\) : one-hot vector of EOS (end of the sentence)
\[\begin{align} \mathbf{X} &= (\mathbf{x}_1, ..., \mathbf{x}_I ) \\ \mathbf{Y} &= (\mathbf{y}_1, ..., \mathbf{y}_J ) \end{align}\]

Conditional Probability of Seq2Seq (skippable)

Conditional probability로 표현을 한다면 \(P(\mathbf{Y} | \mathbf{X})\) 로 나타낼 수 있습니다.
하지만 정확하게 나타내자면 다음과 같습니다.

\[P(\mathbf{Y} | \mathbf{X}) = \prod^{J+1}_{j=1} P_{\theta}\left(\mathbf{y}_j | \mathbf{Y}_{1:j-1}, \mathbf{X} \right)\]

조금 설명을 하자면, \(\mathbf{Y}_{1:j-1}\) 는 바로 output으로 나온 결과값을 사용해서 그 다음 나올 \(\mathbf{y}_j\) 의 값을 예측 한다는 것으로 해석하면 됩니다.
\(P_\theta\) 는 DNN으로 확률을 뽑겠다는 뜻이고, \(\prod\) 를 통해서 전체 확률들을 곱해준것으로 해석하면 됩니다.
즉 저 위에서 그림으로 설명한 내용을 확률 표현식으로 표현한것 뿐입니다. 뭐 없습니다 ㅎ (그림은 참 쉬운데, 수학으로 표현하니 어렵기만 하죠. 별것도 아닌데)

Steps in Seq2Seq Algorithm (skippable)

단순한 구조만큼 쉽습니다.

  1. Encoder는 fixed-size vector \(\mathbf{z}\) 를 \(\mathbf{X}\) 로 부터 생성합니다.
  2. Decoder는 \(\mathbf{z}\) 를 사용해서 \(\mathbf{Y}\) 를 생성합니다.

먼저 1번의 \(\mathbf{z}\) 를 생성하는 함수를 \(\Lambda\) 라고 했을때 수식은 다음과 같으며, 보통 RNN, LSTM등을 사용합니다.

\[\bf{z} = \Lambda({\bf{X}})\]

두번째로, Decoder는 \(\bf{z}\) 로 부터 \(\bf{Y}\) 값을 생성합니다.

\[\begin{align} \bf{h}^{O}_j &= \phi\left( \bf{h}^{(O)}_{j-1}, \bf{y}_j \right) \\ P_{\theta}\left(\bf{y}_j | \bf{Y}_{1:j-1}, \bf{X} \right) &= \gamma \left( \bf{h}^{(O)}_j, \bf{y}_j \right) \end{align}\]
  • \(\phi\) : hidden state를 계산하는 함수입니다.
  • \(\gamma\) : \(\bf{y}\) 의 확률값을 구하는 함수 입니다. (말그대로 확률값이기때문에 argmax같은것으로 취해서 단어로 만들면 됨)

The problem of Seq2Seq

앞서 언급했듯이, Seq2Seq모델은 encoder 그리고 decoder로 이루어져 있습니다.
encoder의 마지막 hidden state가 decoder의 초기 hiddent state로 사용이 됩니다.

바로 유추해볼수 있는 내용은, 만약에 encoder의 sequence data의 길이 가 매우 길 경우..
관련된 정보는 매우 양이 많은데 비해서 그 내용을 함축적으로 하나의 hidden state로 넣는다면 정보의 손실이 있을수 있으며,
이는 곧 catastrophic forgetting 현상으로 이어질수 있습니다.

이러한 문제를 해결하기 위해서 Attention을 사용해서 문제를 해결할수 있습니다.

Seq2Seq Network and Attention Model

Alignment

Alignment 의 정의는 원래의 문장에서, 대응하는 번역된 단어와 일치시키는 것을 의미합니다.

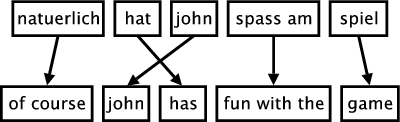
image source: http://www.statmt.org/moses/?n=Moses.Background

Attention

Seq2Seq의 장문일 경우 catastrophic forgetting 문제가 일어나는 현상을 막는데, Attention mechanism 이 도움이 될 수 있습니다.
아래의 그림은 Attn: Illustrated Attention에서 가져온 그림입니다.

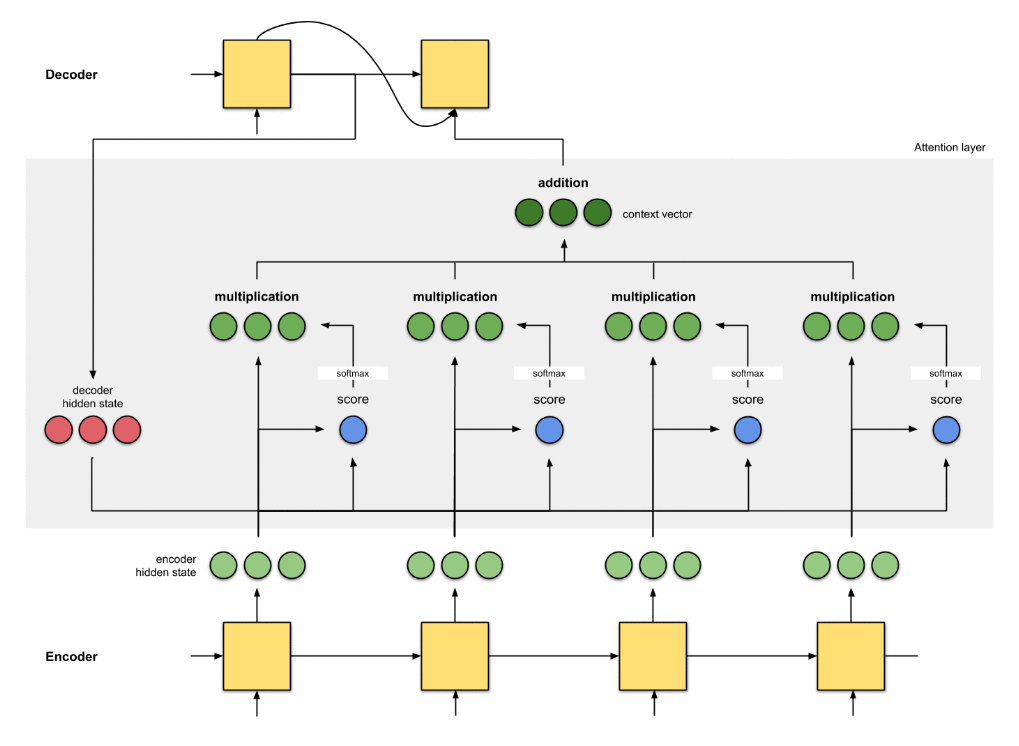
image source: https://towardsdatascience.com/attn-illustrated-attention-5ec4ad276ee3

쉽게 설명하면..

  1. encoder에서 각 input마다의 hidden state를 만듭니다.
  2. alignment score를 계산합니다. (ex. dot(decoder_hidden_state_j, encoder_hidden_states))
  3. align scores에 softmax 함수를 계산
  4. softmax * encoder hidden state 를 해서 softmax score가 높을수록 살리고, 낮으면 죽여버립니다. (Kill!!)
  5. 모든 hidden states를 addition/concat 으로 조합한후 (논문마다 다양) context vector 를 만듭니다.
  6. 만들어진 context vector는 decoder의 input으로 들어가게 됩니다.

Examples

Hidden States

예를 들어서 다음과 같은 encoder hidden states 가 존재합니다.

        word            encoder_hidden
0          I  [0.01, 0.03, 0.11, 0.05]
1      drank  [1.35, 0.04, 1.09, 2.34]
2       milk  [0.34, 0.59, 0.94, 0.96]
3  yesterday  [0.02, 2.12, 0.14, 0.21]

그리고 현재 Decoder의 hidden state는 [1.32, 0.03, 0.56, 0.91] 입니다.

Alignment Score

alignment score를 구하는 방법은 많습니다.
단순히 dot product 를 할수도 있고, cosine distance를 계산해도 됩니다.
예제에서는 decoder hidden state와 encoder hidden states를 dot product합니다.

        word            encoder_hidden                              alignment score
0          I  [0.01, 0.03, 0.11, 0.05] @ [1.32, 0.03, 0.56, 0.91]              0.12
1      drank  [1.35, 0.04, 1.09, 2.34]                                         4.52
2       milk  [0.34, 0.59, 0.94, 0.96]                                         1.87
3  yesterday  [0.02, 2.12, 0.14, 0.21]                                         0.36

Softmax

alignment score에 softmax 를 계산합니다.

        word            encoder_hidden  alignment score  softmax score
0          I  [0.01, 0.03, 0.11, 0.05]             0.12           0.01
1      drank  [1.35, 0.04, 1.09, 2.34]             4.52           0.91
2       milk  [0.34, 0.59, 0.94, 0.96]             1.87           0.06
3  yesterday  [0.02, 2.12, 0.14, 0.21]             0.36           0.01

Multiply softmax by encoder_state

softmax score를 각 encoder hidden states에 곱해줘서 alignment vector를 만들어 줍니다.

        word            encoder_hidden  alignment score  softmax score          alignment vector
0          I  [0.01, 0.03, 0.11, 0.05]             0.12           0.01  [ 0.0, 0.03, 0.01,  0.0]
1      drank  [1.35, 0.04, 1.09, 2.34]             4.52           0.91  [0.02, 0.04, 0.07, 0.03]
2       milk  [0.34, 0.59, 0.94, 0.96]             1.87           0.06  [ 0.0, 0.54, 0.06, 0.01]
3  yesterday  [0.02, 2.12, 0.14, 0.21]             0.36           0.01  [ 0.0, 1.93, 0.01,  0.0]

Context Vector

최종적으로 context vector를 만들어주는데, alignment vectors를 모두 합해서 만듭니다.
즉 encoder에서 처리한 모든 문장에 대한 단어의 정보가 포함되지만, alignment 를 통해서 특정 정보의 가중치를 더 주는 형태입니다.

context vector = [0.02, 2.54, 0.15, 0.04]

이렇게 만들어진 context vector는 decoder의 hidden state와 함께 사용되서 다음 단어를 예측하는데 사용이 됩니다.

Mathematical Explanation

Alignment Score

decoder 의 hiddent state 와 encoder의 hidden states 에 대해서 scoring을 합니다.
위의 예제에서는 단순히 dot product를 사용했지만, 사실 많은 scoring방법이 존재하며, 이에 관해서 논문또한 많습니다.

\[\text{score} (\bf{h}^{(O)}_{j-1}, \bf{h}^{I}_i) = \mathbf{v}_a^\top \tanh(\mathbf{W}_a[\bf{h}^{(O)}_j; \bf{h}^{(I)}_i])\]
  • \(\bf{h}^{(O)}_{j-1}\) : Decoder의 이전 hidden state (예제. decoder hidden state = [1.32, 0.03, 0.56, 0.91])
  • \(\bf{h}^{(I)}_i\) : Encoder의 hidden state
  • \(\bf{v}_a\) : weight matrix in the alignment model
  • \(\bf{W}_a\) : weight matrix in the alignment model

다양한 Attention Mechanisms 은 링크 에서 가져온 내용을 첨부합니다.

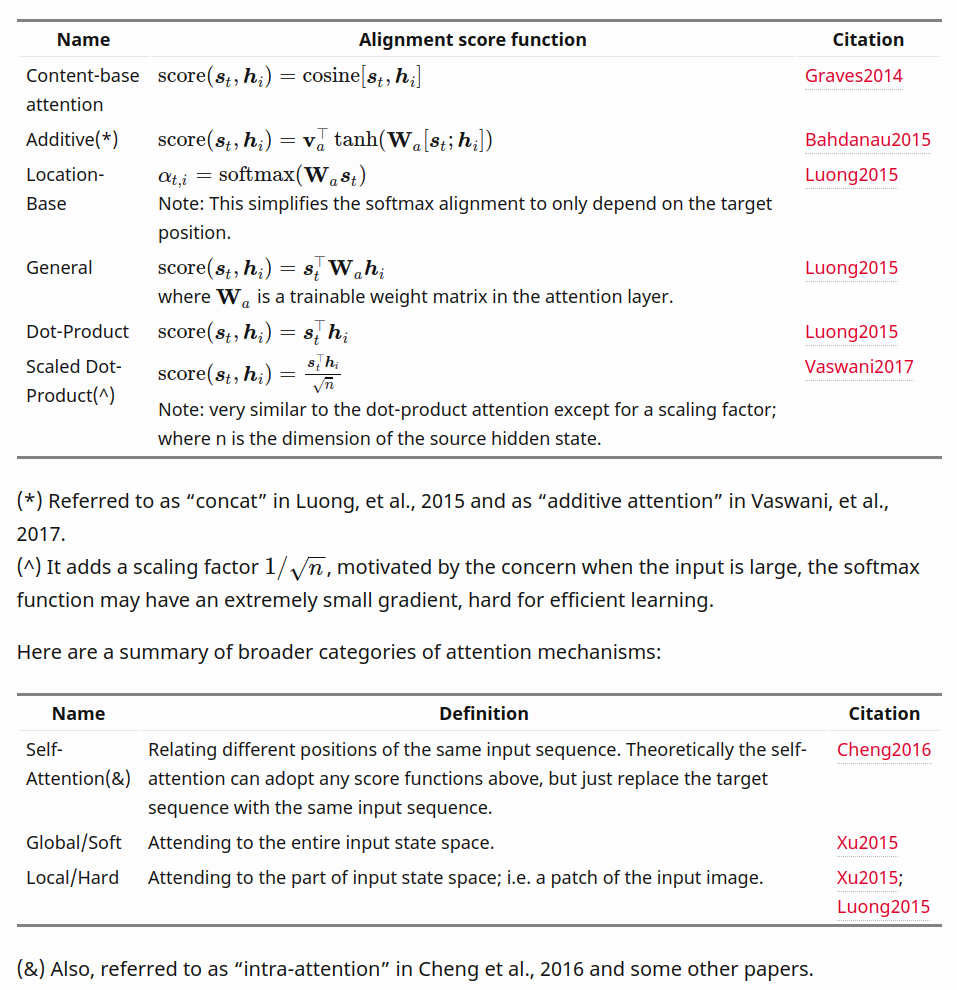
image source: https://lilianweng.github.io/lil-log/2018/06/24/attention-attention.html

제가 본문에서 사용한 수리적 기호가 다른데, 다음과 같습니다.

  • \(\bf{s}_t\) : Decoder의 특정 hidden state
  • \(\bf{h}_i\) : Encoder의 특정 hidden state

### Softmax Score

\[\begin{align} \alpha_{j, i} &= align(y_j, x_i) \\ &= \frac{\exp \left(\text{score} \left(\bf{h}^{(O)}_{j-1}, \bf{h}^{(I)}_i \right) \right)}{\sum^n_{i=1} \exp\left(\text{score} \left(\bf{h}^{(O)}_{j-1}, \bf{h}^{(I)}_i \right) \right)} \end{align}\]

예제에서는 softmax score라고 적었지만, 사실상 여기까지를 ailgnment score라고 봐도 됩니다. (편의상 softmax score라고 하겠습니다)
dot product한후, 이것을 softmax로 확률로 표현해준 것 뿐입니다.

  • \(align(y_j, x_i)\) : decoder 단어 \(y_j\) 그리고 encoder 단어 \(x_i\) 이 서로 얼마나 alignemnt 가 맞는지를 수치화 한 것입니다. (좀 추상적인 표현)
  • \(softmax\) : 그 아래에 실제 구현 방법으로 softmax를 사용했습니다.

Context Vector

최종 context vector 는 softmax score와 Encoder 의 hidden states를 곱해서 모두 합한 값입니다.

\[\bf{c}_j = \sum^n_{i=1} \alpha_{j, i} \bf{h}^{(O)}\]

예제에서는.. 최종적으로 context vector = [0.02, 2.54, 0.15, 0.04] 이렇게 나왔습니다.