Sentence Bert
1. Problem
2. Summary
- 2.1 BERT VS Sentence-BERT (SBERT)
- 2.1 Model
3. Model in Detail

Sentence Bert

Key	Value
Paper	https://arxiv.org/pdf/1908.10084
publication Date	2019

1. Problem

상황

문장 A 가 있을때 B1 ~ B10,000 까지 1만개의 문장이 있음
이때 A와 가장 유사한 단어를 찾고 싶은 것임

기존 BERT 방식

BERT는 문장을 “[CLS] A문장 [SEP] B문장” 형태로 합쳐서 넣고
두 쌍을 BERT에 통채로 넣어서 inference를 함
즉 training 시에 모든 문장의 유사도 계산시 10,000 x 9,999 번의 계산이 필요함
따라서 매우 비효율적임

2. Summary

2.1 BERT VS Sentence-BERT (SBERT)

Key	BERT	Setence-BERT (SBERT)
input method	Cross Encoder 방식 - “[CLS] A 문장 [SEP] B 문장”	각 문장을 따로따로 입력 (Bi-Encoder)
Embedding Generation	토큰 단위 (shape: [1, seq_len, 768])	문장 전체를 하나의 벡터로 유지 (shape: [384,] <- 벡터 하나)
Performance	Cross Encoder 방식이 더 정확함. 하지만 느림	정확도가 꽤나 잘 유지, 매우 빠름, 특히 검색에서 좋음
Architecture	단일 Transformer	Siamese 또는 Triplet Network
Usage	Classification, QnA, NLI	Similarity Search, Clustering, Recommendation

2.1 Model

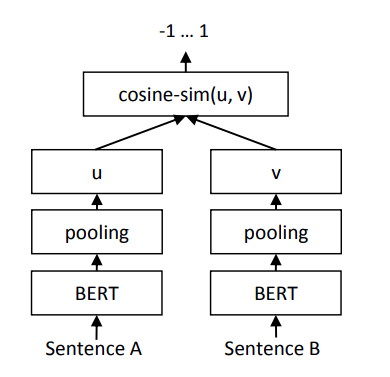
특징

BERT 또는 RoBERTa 에 적용 가능
Pooling 사용하여 fixed sized sentence embedding 생성
Pooling Method
- CLS Pooling: last_hidden_state[:, 0, :] # shape (1, hidden_dim)
- Mean Pooling: [PAD] Token을 제외하고 평균을 냄. SBERT 의 기본값
- MAX Pooling: [PAD] 부분은 음수로 바꾸고 나머지에서 MAX를 취함
Training Method: Siamese, Triplet Loss
Performance: Bi-Encoder 를 사용함으로서 빠른 유사도 계산 가능

3. Model in Detail

3.1 Forward Triplet

    def forward_triplet(self, input_ids_a, attention_mask_a, 
                       input_ids_p, attention_mask_p,
                       input_ids_n, attention_mask_n):
        """
        Forward pass for triplet loss
        Paper: max(||sa − sp|| − ||sa − sn|| + ε, 0)
        
        Args:
            input_ids_a, attention_mask_a: anchor sentence
            input_ids_p, attention_mask_p: positive sentence  
            input_ids_n, attention_mask_n: negative sentence
        """
        # Anchor sentence encoding
        outputs_a = self.bert(input_ids=input_ids_a, attention_mask=attention_mask_a)
        embeddings_a = self.mean_pooling(outputs_a.last_hidden_state, attention_mask_a)
        embeddings_a = self.pooling(embeddings_a)
        embeddings_a = self.dropout(embeddings_a)
        
        # Positive sentence encoding
        outputs_p = self.bert(input_ids=input_ids_p, attention_mask=attention_mask_p)
        embeddings_p = self.mean_pooling(outputs_p.last_hidden_state, attention_mask_p)
        embeddings_p = self.pooling(embeddings_p)
        embeddings_p = self.dropout(embeddings_p)
        
        # Negative sentence encoding
        outputs_n = self.bert(input_ids=input_ids_n, attention_mask=attention_mask_n)
        embeddings_n = self.mean_pooling(outputs_n.last_hidden_state, attention_mask_n)
        embeddings_n = self.pooling(embeddings_n)
        embeddings_n = self.dropout(embeddings_n)
        
        return embeddings_a, embeddings_p, embeddings_n

3.2 Forward Classification

논문에서는 Sentence-Pair Classification을 다음과 같이 설명합니다.

For classification tasks, we feed the concatenation of u, v, and |u−v| into a classification layer

\[\begin{align} h &= \left[u; v; |u-v| \right] \\ p &= softmax(W \dot h + b) \end{align}\]

쉽게 말해서

u: 첫번째 문장의 임베딩
v: 두번째 문장의 임베딩
| u-v | : 두 임베딩의 절댓값 차이
h: [u, v, | u-v |] 형태로 concatenate
p: softmax(Wt(h) + b) 형태로 분류

    def forward(self, input_ids_1, attention_mask_1, input_ids_2, attention_mask_2):
        """
        Forward pass for sentence pair classification
        """
        # Encode first sentence
        outputs_1 = self.bert(input_ids=input_ids_1, attention_mask=attention_mask_1)
        embeddings_1 = self.mean_pooling(outputs_1.last_hidden_state, attention_mask_1)
        embeddings_1 = self.pooling(embeddings_1)
        embeddings_1 = self.dropout(embeddings_1)
        
        # Encode second sentence
        outputs_2 = self.bert(input_ids=input_ids_2, attention_mask=attention_mask_2)
        embeddings_2 = self.mean_pooling(outputs_2.last_hidden_state, attention_mask_2)
        embeddings_2 = self.pooling(embeddings_2)
        embeddings_2 = self.dropout(embeddings_2)
        
        # Calculate absolute difference between sentence pairs (SNLI paper method: u, v, |u-v|)
        diff = torch.abs(embeddings_1 - embeddings_2)
        
        # Concatenate for classification (paper implementation: u, v, |u-v|)
        combined = torch.cat([embeddings_1, embeddings_2, diff], dim=1)
        
        # Classification (input dimension: 3n → k)
        logits = self.classifier(combined)
        
        return logits, embeddings_1, embeddings_2

3.2 Mean Pooling

논문에서는 Mean Pooling을 사용하여 문장 임베딩을 생성함

“We experiment with three different pooling strategies: [CLS] token, mean of the last layer output, and max-over-time pooling.” In our experiments, mean pooling over the token embeddings worked best.

구현은 다음과 같이 함.

쉽게 설명하면

BERT의 last_hidden_state 를 가져옴 (전체 토큰의 임베딩)
[PAD] 토큰은 제외하고 나머지 토큰들의 평균을 구함
이때 attention mask를 사용하여 [PAD] 토큰을 제외함

    def mean_pooling(self, token_embeddings, attention_mask):
        """
        Mean pooling: calculate average considering attention mask
        """

        # [batch_size, seq_len] → [batch_size, seq_len, hidden_dim]
        # (64, 768) -> (64, 160, 768)
        input_mask_expanded = attention_mask.unsqueeze(-1).expand(token_embeddings.size()).float()

        # [batch_size, hidden_dim] (32, 768) = token_embeddings (32, 160, 768) * input_mask_expanded (32, 160, 1)
        sum_embeddings = torch.sum(token_embeddings * input_mask_expanded, dim=1)
        # [batch_size, hidden_dim] (32, 768) = sum_embeddings (32, 768) / input_mask_expanded.sum(dim=1) (32, 768)
        sum_mask = torch.clamp(input_mask_expanded.sum(dim=1), min=1e-9)
        return sum_embeddings / sum_mask

이후에 forward에서는 다음과 같이 embedding 을 만듭니다.

    def forward_triplet(self, input_ids_a, attention_mask_a, 
                       input_ids_p, attention_mask_p,
                       input_ids_n, attention_mask_n):
        # Anchor sentence encoding
        outputs_a = self.bert(input_ids=input_ids_a, attention_mask=attention_mask_a)
        embeddings_a = self.mean_pooling(outputs_a.last_hidden_state, attention_mask_a)
        embeddings_a = self.pooling(embeddings_a)
        embeddings_a = self.dropout(embeddings_a)
        
        # skip...

self.pooling = nn.Linear(embedding_dim, embedding_dim) 입니다. 논문에서는 나온 따로 linear layer를 사용하는 내용은 따로 없지만, 실용적으로 자주 사용되는 방법입니다.

3.3 Siamese Network

Siamese Network (샴 네트워크)는 두개 이상의 입력 (두 문장, 두 이미지)를 동일한 모델에 넣어 각각의 embedding을 만든후, 두 embeddings 의 유사도를 계산하는 구조

수학적 정리

동일한 신경만 f(x) 를 두번 사용
유사도 계산
- Cosine Similarity: \(cosine \left( f(x_1), f(x_2) \right) = \frac{ f(x_1) \dot f(x_2)}{ \| f(x_1) \| \| f(x_2) \| }\)
- Euclid Distance: \(\| f(x_1) - f(x_2) \|_2\)

1.5.1 Cosine Similarity + MSE Loss (Regression Loss)

\[Loss = MSE(cos(u, v), label)\]

Example

문장 A: “The Cat is sleeping”
문장 B: “A feline is resting”
label = 4.5/5 = 0.9
cosine(u, v) 가 0.9에 맞도록 학습

import torch
import torch.nn.functional as F

u = torch.randn(1, 768)  # sentence A
v = torch.randn(1, 768)  # sentence B

# Cosine similarity: [-1, 1]
cos_sim = F.cosine_similarity(u, v)

label = torch.tensor([0.85]) 
mse_loss = F.mse_loss(cos_sim, label)
print("MSE Loss:", mse_loss.item())

1.5.2 Classification Objective

\[\begin{align} h &= \left[ u; v;; | u -v | \right] \\ o &= softmax(W_t \dot h + b) \\ L &= CrossEntropy(o, y) \end{align}\]

y 는 0, 1 같은 binary classification label
\(u, v \in \mathbb{R}^n\) : 두 문장의 embeddings
\(abs( u - v )\) : element-wise 절대값 차이
\(h \in \mathbb{R}^{3n \time k}\) 3개의 vector를 concatenate 함 torch.cat([u, v, torch.abs(u - v), dim=1)

이후에 Cross Entropy Loss 사용 코드상에서는 그냥 nn.CrossEntropyLoss() 를 사용하면 됩니다.

    def forward(self, input_ids_1, attention_mask_1, input_ids_2, attention_mask_2):
        # skip.. 
        
        # Calculate absolute difference between sentence pairs (SNLI paper method: u, v, |u-v|)
        # Concatenate for classification (paper implementation: u, v, |u-v|)
        diff = torch.abs(embeddings_1 - embeddings_2)
        combined = torch.cat([embeddings_1, embeddings_2, diff], dim=1)
        
        # Classification (input dimension: 3n → k)
        logits = self.classifier(combined)

criterion = nn.CrossEntropyLoss()
# skip..
loss = criterion(logits, labels)

1.5.3 Triplet Loss

\[TripletLoss = max(\| s_a - s_p \| - \| s_a - s_n \| + \epsilon, 0)\]

\(s_a\) : anchor 문장의 embedding
\(s_p\) : positive 문장의 embedding
\(s_n\) : negative 문장의 embedding
\(\epsilon\) : margin 이고 논문에서는 1로 설정
- 두 embeddings 사이의 최소 거리가 1이

예제 1: 서로 잘 분리 되어 있음으로 loss가 0이 됨

\[\begin{align} | s_a - s_p | &= 1.0 \\ | s_a - s_n | &= 2.5 \\ loss &= max(1.0 - 2.5 + 1, 0) = max(-0.5, 0) = 0 \end{align}\]

예제 2: 서로 가까이 붙어 있음으로 loss가 0.8이 발생됨

\[\begin{align} | s_a - s_p | &= 1.0 \\ | s_a - s_n | &= 1.2 \\ loss &= max(1.0 - 1.2 + 1, 0) = max(0.8, 0) = 0.8 \end{align}\]

코드상에서는

def triplet_loss(embeddings_a, embeddings_p, embeddings_n, margin=1.0):
    """
    Calculate triplet loss
    Paper: max(||sa − sp|| − ||sa − sn|| + ε, 0)
    
    Args:
        embeddings_a: anchor sentence embeddings
        embeddings_p: positive sentence embeddings
        embeddings_n: negative sentence embeddings
        margin: margin ε (set to 1 in paper)
    
    Returns:
        triplet_loss: calculated triplet loss
    """
    # Calculate Euclidean distance
    # ||sa - sp||
    # torch.norm = L2 norm (Euclidean distance)
    dist_pos = torch.norm(embeddings_a - embeddings_p, p=2, dim=1)
    
    # ||sa - sn||
    dist_neg = torch.norm(embeddings_a - embeddings_n, p=2, dim=1)
    
    # max(||sa − sp|| − ||sa − sn|| + ε, 0)
    triplet_loss = torch.clamp(dist_pos - dist_neg + margin, min=0.0)
    
    return triplet_loss.mean()