Monte Carlo Tree Search
Introduction
알파제로를 설명하기 위한 기초단계로서 Monte Carlo Tree Search를 소개합니다.
위의 게임은 Tic Tac Toe 게임으로서 인간 VS 컴퓨터와의 대결을 보여줍니다.
결론만 말하면, 이 게임에서 둘다 잘한다면 누구도 이길수 없게 됩니다.
Monte Carlo Tree Search (이하 MCTS)를 사용하면 multi-stage 환경 (턴제 게임같은..)에서 Markov Decision Process같은 모델을 만들 수 있습니다. 가장 중요한 핵심은 Multi-Armed Badit 문제처럼, exploration과 exploitation을 잘 활용해야 하는데, 이 문제를 MCTS를 사용해서 해결이 가능합니다.
Steps of MCTS
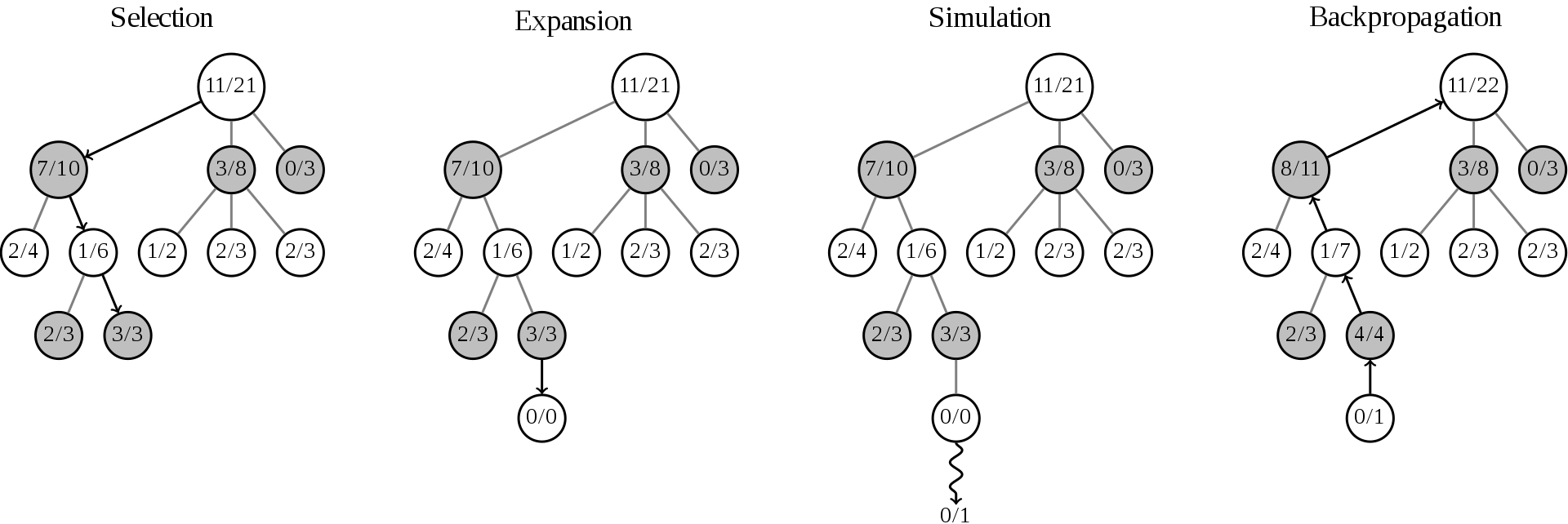
Selection
Root node에서 시작을 해서 child node를 타고 타고 내려가기 시작합니다.
타고 타고 내려가다가 트리의 끝인 leaf node에 도착하게 되면 selection은 멈추게 됩니다.
트리를 traversal할때 중요한 2가지 항목을 만족시켜야 합니다.
첫번재는 exploration으로서 아직 가보지 않은 길을 감으로서 새로운 정보를 얻습니다.
두번째는 exploitation으로서 기존의 정보를 이용하여 좋은 길(child node)을 선택하는 것입니다.
따라서 selection function은 이 두가지 exploration과 exploitation을 최적으로 만족시키는 방식을 취해야 합니다.
이때 사용하는 방식이 바로 UCB1(Upper Confidence Bound 1)이라는 함수인데,
이 함수가 MCTS와 함께 사용된 알고리즘이 바로 UCT (Upper Confidence Bound 1 applied to Trees)라는 함수 입니다.
공식은 다음과 같습니다.
- \(\frac{w_i}{n_i}\): exploitation component라고 하며, winning/losing 의 비율
- \(w_i\): i번째 자식 노드의 이긴 횟수 (number of wins)
- \(n_i\): i번째 자식 노드의 방문 횟수 또는 시뮬레이션 횟수 (number of simulations)
- \(\sqrt{ \frac{\ln t}{ n_i}}\): exploration component라고 하며, exploitation component만 사용하게 되면 오직 simulation에서 이겼던 기록이 있는 노들만 따라가기 때문에 생겨나는 문제를 해결.
- \(t\): 부모(현재) 노드의 방문 회수 또는 시뮬레이션 횟수 (number of simulations for the parent node)
- \(c\): exploration component의 가중치로 생각하면 되며 보통 \(\sqrt{2}\) 를 사용
UCT를 사용하지 않고 단순 랜덤으로 선택을 할 경우 exploration에는 매우 좋지만, 기존의 정보를 활용하는 exploitation에는 매우 안 좋습니다. 또한 각각의 node마다의 평균 승률을 사용하는 방법은 exploitation에 좋지만, exploration에는 좋은 방법이 아닙니다.
exploration component의 직관적인 이해는 방문이 상대적으로 적은 노드를 선택하도록 유도를 하게 됩니다.
예를 들어서 아래의 경우 현재 노드 (부모 노드)의 방문 t=5000 일때, 자식노드의 방문횟수에 따른 그래프는 다음과 같습니다.
def exploration_component(t, x):
c = np.sqrt(2)
return c * np.sqrt(np.log(t) / (x+1))
x = np.arange(0, 100)
y = exploration_component(t=500, x=x)
lp = sns.lineplot(x, y, label='parent visit count. t=500')
lp.set(xlabel='child visit count', ylabel='exploration')
grid()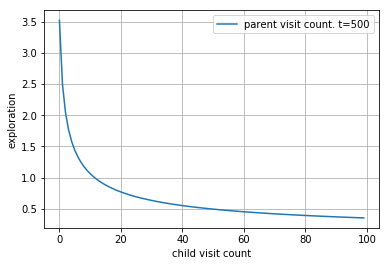
즉 매우 드물게 방문한 노드(액션)일수록 선택할 확률값이 올라가게 됩니다.
Expansion
Selection에 leaf node에 도착해서 멈추게 되면, 최소한 한개의 가보지 않은 move (또는 action)이 있을 것 입니다.
이때는 그냥 랜덤으로 unexpanded move를 선택하고 새로운 child node를 생성합니다.
해당 child node는 selection phase에서 중단된 마지막 leaf node에 자식노드로 연결을 시킵니다.
child node의 초기화 세팅은 승률은 \(w_i = 0\), 그리고 방문 횟수는 \(n_i = 0\) 으로 초기화 시킵니다.
구현상의 중요 포인트는, expansion시에 모든 action (또는 move)에 대해서 한꺼번에 만들어줄 필요는 없습니다.
expansion마다 하나의 child node를 만들어주는게 효율적입니다.
Simulation
자~ expansion phase에서 새롭게 만들어진 자식노드에서 계속 진행하겠습니다.
정말 쉽게 설명하기 위해서 엔지니어적으로 설명하면.. 현재 상태의 트리를 하나 더 복사합니다.
그리고 selection 그리고 expansion을 전에 새롭게 만들어진 자식 노드에서 k번 반복시킵니다.
즉.. 랜덤으로 하나 move를 선택하고 다시 expansion하고 또 랜덤으로 하나 move를 선택하고 다시 expansion하고..
이 과정을 복사된 트리에서 진행을 합니다. (즉 원본 트리는 변경된 내용이 전혀 없습니다)
또한 그 과정은 게임을 끝날때까지 k번 반복 시킵니다.
문제만다 다르기는 하지만.. 일반적으로 빠르게 학습시키기 위해서 k=1 로 설정을 하기도 합니다.
다만 예측률을 극도로 높이고 할때는 k를 높이면 되고, 실제 AlphaGo의 경우 한번의 simulation마다 k=1600 으로 하기도 했으며, AlphaZero의 경우 k=800으로 했다고 페이퍼에서 말하고 있습니다. (Paper: “During training, each MCTS used 800 simulations”)
또한 simulation 자체가 극단적으로 큰 computation power를 요구하기 때문에 엔지니어링적으로 효율적으로 돌릴수 있도록 멀티쓰레드 또는 distributed computation을 적극적으로 활용해야 합니다.
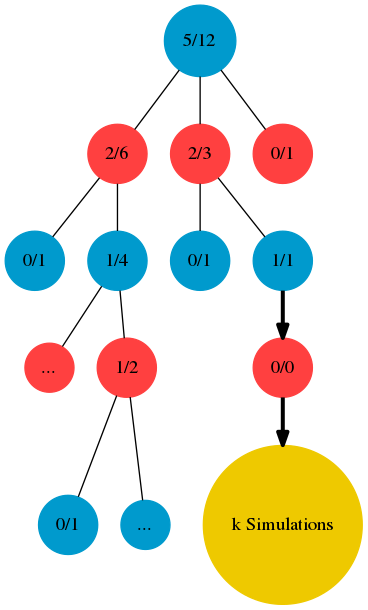
Backpropagation
Simulation phase가 k번 돌고 완료된 후, selection에서 중단된 leaf node의 부모노드 -> 부모노드 -> 부모노드 계속 타고 가면서 업데이트를 시켜줍니다. 자! 무엇을 업데이트 시키냐하면.. 방문 횟수 \(n_i = k\) (simulation돌린만큼 방문횟수를 증가시킴) 그리고 이긴 횟수를 증가시켜야 되는데.. 여기서 좀 복잡합니다.
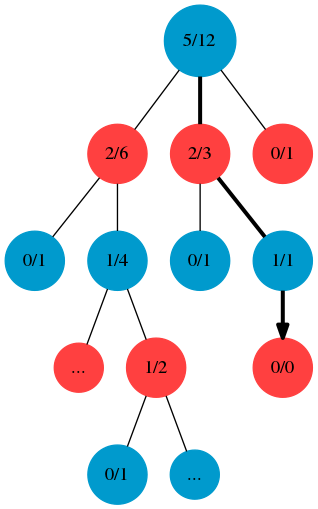
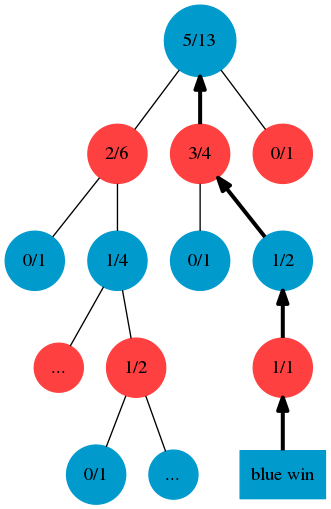
아래 그래프에서 보면, Blue가 이겼습니다.
방문횟수는 backprogagation을 하면서 모든 parent nodes를 k simulation만큼 증가 시켜주었는데,
이긴 횟수는 red쪽이 증가 되었습니다.
상식적으로는 blue가 이겼으니까, blue node의 이긴 횟수가 증가되어야 할거 같지만,
예를 들어 Blue node에 있을때, 어떤 자식 노드들(Red)를 선택해야지 Blue가 이길확률이 높일지를 생각해봤을때..
Blue의 자식노드들인 Red에다가 이긴 횟수를 증가시켜주는 것이 맞습니다.
UCT공식을 생각하면 당연한 것이 되죠.
In Practice
실제 MCTS를 구현하는 방식에는 많은 방법들이 존재합니다.
몇가지 구현방법을 소개하면 다음과 같습니다.
1. 그래프 구조로 구현
그래프 구조로 구현한다는 뜻은 뭐 특별한 것이 아니라 Dictionary (Hash Table)을 사용해서 구현을 합니다.
이때 key값은 state값이 들어가고, value값에는 children과 action이 함께 가져가는 구조입니다.
예를 들어서 다음과 같습니다.
nodes = {state1: {state3: action1, state4: action4},
state2: {state1: action2},
state3: {state5: action3, state1: action1}
....
}2. Simulation 제거
꼭 페이퍼에서 말하는대로 할 필요는 없습니다.
핵심은 UCT 함수를 통해서 exploration과 exploitation을 잘 한다는 것이고, 게임 한번 쭉 돌고 마지막에 한번 backpropagtion을 하는 것도 방법입니다. 이렇게 해주면 simulation이 없어지기 때문에 학습의 속도가 빨라지게 됩니다.
Simulation이 도는 조건은 구현마다 다를 수 있습니다.
- Leaf node에 도착하게 되면 expasion후 k번 simulation돌려서 그 결과값을 backpropagation한다 -> 원래 방법
- selection할때 leaf node까지 가는게 아니라, next state로 넘어갈때마다 simulation을 해준다 -> 비효율적
- Simulation을 제거해버리고, backpropagation은 게임이 끝난 마지막에 한다 -> 실용적