기본적인 구조

의학 이미지안에서 질병등을 발견하는 것은 매우 중요합니다.
Anomaly Detection GAN은 Discriminator를 통해서 의학 이미지 상에서 질병을 찾아내도록 도와줍니다.
물론 Anomaly라는 개념하에서 반드시 질병일 필요는 없습니다.

기본적인 구조는 아래와 같으며, Deep Convolutional Generative Adversarial Network (DCGAN)을 사용했으며,
오른쪽 그림은 t-SNE embedding으로 파란색은 정상, 빨간색은 비정상(anomalous images) 를 나타냅니다.

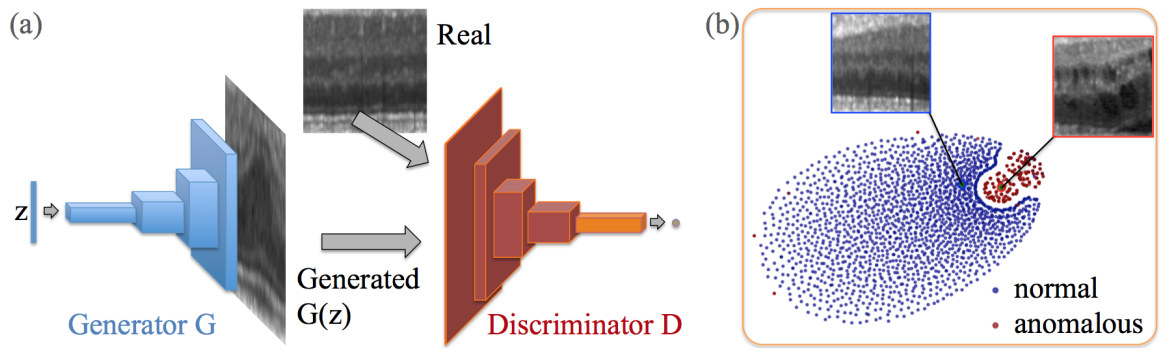
  • Medical Images: \(\mathbf{I}_m\) 으로서 \(m = 1,2,..., M\) 이며, 모두 정상적인 상태의 (질병이 없는) 이미지, \(\mathbf{I}_m \in \mathbb{R}^{a*b}\) 입니다.

학습시에는 오직 \(\mathbf{I}_m\) (질병없는 정상 이미지)가 주어지며, 해당 이미지로부터 c x c 크기의 image patch \(x_{k,m}\) 를 랜덤으로 위치를 샘플링해서 추출하게 됩니다. 즉, \(\mathbf{x} = x_{k,m} \in \mathcal{X}\) 이며, 쉽게 설명하면 큰 메디컬 사진안에서 c x c 크기의 일부구간을 랜덤으로 잘라내고, 잘라진 구간을 비젼에서는 image patch 라고 말하며, 해당 image patch 는 질병이 없는 (위의 파란색) manifold \(\mathcal{X}\) 를 학습한다는 뜻입니다.

테스트시에는 \(\mathbf{y}_n, l_n\) 이 주어지며, \(\mathbf{y}_n\) 은 testing data \(\mathbf{J}\) 의 c x c 싸이즈의 이미지입니다.
\(l_n \in \{0, 1\}\) 은 바이너리 값으로서 레이블값이라고 생각하면 되며, 오직 테스트를 할때만 정말 잘 되는지 판단하기 위해서 주어지는 값입니다.

GAN 복습

기본적인 GAN을 복습하는 차원에서 보도록 하겠습니다. (anomaly detection의 관점에서)
GAN은 아시다시피 2개의 적대적인 모듈로 이루어 져 있습니다.

  • Discriminator \(G\) : \(G(\mathbf{z}) : \mathbf{z} \rightarrow \mathbf{x}\) 매핑을 통하여 정상적 데이터 (질병이 없는) \(\mathbf{x}\) 로 부터 distribution \(p_g\) 를 학습하며 1D -> 2D 이미지가 됩니다.
  • samples \(\mathbf{z}\) : 1차원의 vector라고 하면 되며, uniform distribution을 따르는 noise라고 생각하면 되며 Latent space \(\mathcal{Z}\) 로부터 샘플이 취해졌습니다.
  • Image patch \(\mathbf{x}\) : 질병이 없는 정상적인 메디컬 사진에서 랜덤으로 c x c 싸이즈로 샘플링한 이미지이며, image space manifold \(\mathcal{X}\) 안에 속한다고 봅니다.

이러한 설정안에서, Generator \(G\) 는 convolutional decoder라고 보면 되며, 여러층을 쌓은 (stack) strided convolutions입니다.
Discriminator \(D\) 는 일반적인 CNN이며 2D images를 받아서 scalar value \(D(\cdot)\) 으로 매핑합니다.
결론적으로 Minimax game 을 통해 학습되며 Value function \(V(G, D)\) 는 다음과 같습니다.

\[\min_G \max_D V(D, G) = \mathbb{E}_{\mathbf{x} \sim P_{data}(\mathbf{x})} \big[ \log D(\mathbf{x}) \big] + \mathbb{E}_{\mathbf{z} \sim P_{\mathbf{z}}(\mathbf{z})} \big[ \log \big( 1- d(G(\mathbf{z})) \big) \big]\]

Discriminator는 위의 공식으로 학습하면 되고, Generator는 minimax에 문제가 좀 있어서 아래와 같이 학습을 하게 됩니다.
자세한 내용은 GAN을 문서를 확인합니다.

\[V(G) = D(G(\mathbf{z}))\]

이미지를 Latent space z 에 매핑하는 방법

GAN학습이 완료되면 Generator는 \(G(\mathbf{z}) = \mathbf{z} \rightarrow \mathbf{x}\) 처럼 latent space \(\mathbf{z}\) 로부터 정상적 메디컬 사진 (질병이 없는) 이미지 \(\mathbf{x}\) 로 매핑을 하게 됩니다.
문제는 그 반대의 상황이 어렵습니다. 즉 \(G^{-1}(\mathbf{x}) = \mathbf{x} \rightarrow \mathbf{z}\) 는 할 수가 없습니다.

Latent space \(z\) 는 smooth transition을 갖습니다..
즉 latent space상에서 가까운 거리의 두 지점을 통해 생성된 이미지는 서로 매우 유사합니다.

UNSUPERVISED REPRESENTATION LEARNING WITH DCGAN 를 참고합니다.

AnoGAN은 query image \(\mathbf{x}\) 가 주어졌을때, 해당 이미지 \(\mathbf{x}\) 와 가장 유사한 이미지 \(G(\mathbf{z})\) 를 생성하는 \(\mathbf{z}\) 를 찾아냅니다.
가장 최적화된 \(\mathbf{z}\) 를 찾기 위해서 다음과 같이 합니다.

  1. G와 D를 normal dataset으로 학습을 완료합니다.
  2. Random sampling으로 \(\mathbf{z}\) 를 생성합니다.
  3. \(G(\mathbf{z}_1)\) 을 통해서 가까 이미지를 생성합니다. (여기서 1은 update iteration의 횟수입니다.)
  4. loss function을 통해서 gradients를 계산하고 backpropagation을 통해서 \(\mathbf{z}\) 를 업데이트 합니다. (이후 \(\mathbf{z}_1, \mathbf{z}_2, \mathbf{z}_3, ..., \mathbf{z}_\Gamma\) 값이 나오게 됩니다. )
    사용되는 loss function은 2개 components로 이루어져 있습니다. (residual loss 그리고 discrimination loss)

Residual Loss

Residual loss는 query image \(\mathbf{x}\) 와 생성된 이미지 \(G(\mathbf{z}_\gamma)\) 의 시각적 차이를 측정하기 위해서 사용이 됩니다.

\[L_R \left(\mathbf{z}_{\gamma} \right) = \sum \big|\ \mathbf{x} - G(\mathbf{z}_\gamma) \ \big|\]

코드는 다음과 같습니다.

def residual_loss(real_y, generated_y):
    return torch.sum(torch.abs(real_y - generated_y))

Discrimination Loss

\[L_{\hat{D}} \big( \mathbf{z}_\gamma \big) = \sigma \big( D(G(\mathbf{z}_\gamma)), \alpha \big)\]
  • Discrimination loss값을 구해서 \(\mathbf{z}_\gamma\) 를 업데트하는데 사용이 됩니다.
  • \(\sigma\) : sigmoid cross entropy
  • \(\alpha = 1\) 이다. 따라서 cross entropy는 실질적으로 \(\sigma \big( 1 \cdot \log (p) \big)\)
  • \(\gamma\) : Update Iteration
  • Semantic Image Inpainting with GAN 논문에서 이미지 복원을 위해 제안된 방법입니다.
    하지만 AnoGAN논문에서는 아래의 Improved Discrimination Loss를 제안하고 있습니다.
  • 한마디로 요약하면, AnoGAN에서는 feature matching기법을 사용하기 때문에, 위의 공식은 안쓰입니다.

Improved Discrimination Loss based on Feature Matching

AnoGAN에서 새로 제안하는 Improved Discriminator Loss 는 다음과 같습니다.

\[L_D(\mathbf{z}_\gamma) = \sum \big\| \mathbf{f}(\mathbf{x}) - \mathbf{f}(G(\mathbf{z}_\gamma)) \big\|\]
  • 마찬가지로 Discrimination loss이지만, discriminator를 업데이트하는게 아니라 \(\mathbf{z}_\gamma\) 를 gradient descent방식으로 업데이트 합니다.
  • \(\mathbf{f}\) : feature mapping에서 나온 개념으로 discriminator의 중간층에 있는 activations들을 가르킵니다.
  • \(\mathbf{z}\) : 그냥 random sampling하면 됩니다.
  • \(\gamma\) : \(\mathbf{z}\) 를 iterate돌면서 (실제로는 backpropagation) 업데이트 시키는 것을 나타냅니다.
  • \(\mathbf{z}\) 를 업데이트하는 동안에는 Generator와 Discriminator를 업데이트 하지 않으며, 이미 train이 완료된 상태어야 합니다.
  • \(\lambda\) : 가중치

Finding the closest mapping : z-> G(z)

Semantic Image Inpainting with GAN 논문을 보면 복원할 이미지와 가장 유사한 이미지를 generate하기위해서, backpropagation 방식으로 \(\mathbf{z}_\gamma\) 를 업데이트 시킵니다.
참고로.. 유사하게 input값을 업데이트 시키는 방식은 Style Transfer 그리고 Deep Dream 등등이 있습니다.

Latent space에 매핑하기 위한 loss function은 residual loss와 improved discriminator 두가지를 weighted sum한 것과 같습니다.

\[L(\mathbf{z}_\gamma) = (1-\lambda) \cdot L_R(\mathbf{z}_\gamma) + \lambda \cdot L_D (\mathbf{z}_\gamma)\]

코드..

def anomaly_loss(residual_loss, d_loss, l=0.5):
    return (1 - l) * residual_loss + l * d_loss

Feature Matching

Improved GAN페이퍼에 따르면, Feature Matching기법은 GAN이 불안정성(instability)를 해결하기 위해서 사용되며,
Discriminator 중간층에 있는 activations들을 사용하여 Generator를 학습시키는데 사용이 됩니다.

이 기법을 사용하면, Generator는 Discriminator 중간층에 있는 activations들의 outputs을 해당 이미지를 나타내는 특정 features들로 봤을때, 실제 이미지와 유사한 features들을 생성하도록 만들수가 있습니다.

즉 원래 GAN에 따르면 Discriminator는 cross entropy loss를 사용해서 실질적으로 이분법적 사고를 하게 됩니다.
진짜냐? 가짜냐?…
진짜냐 가짜냐로 나온 loss값을 사용해서 Generator를 학습시키는 것이 아니라..
실제 이미지의 패턴과 얼마나 유사하냐? 를 물음으로서 좀 더 Generator가 실제 이미지의 패턴과 유사해지도록 만들게 됩니다.

Feature Mapping의 코드는 다음과 같습니다.

def feature_mapping(G, D, real, fake):
    _, real_fs = D.forward(real, _return_activations=True)
    _, fake_fs = D.forward(fake, _return_activations=True)
    real = real_fs
    fake = fake_fs

    diffs = []
    for real, fake in zip(real_fs, fake_fs):
        diff = torch.mean(torch.pow(real - fake, 2))
        diffs.append(diff)

    output = torch.mean(torch.stack(diffs))
    return output

Anomaly Score

비정상 탐지(Anomaly identification)동안에는 새로운 query image \(\mathbf{x}\) 를 정상적인 이미지인지, 또는 비정상적인 이미지인지를 판별하게 됩니다.
위에서 설명한 latent space에 대한 loss function \(L(\mathbf{z}_\gamma)\) 은 매 update iteration \(\gamma\) 마다 \(G(\mathbf{z}_\gamma)\) 과 query image를 비교하게 됩니다.

Anomaly Score는 query image \(\mathbf{x}\) 가 얼마나 정상적인 이미지에 맞는지를 판단하게 되며, 공식은 다음과 같습니다.

\[\begin{align} A(\mathbf{x}) &= (1-\lambda) \cdot R(\mathbf{x}) + \lambda \cdot D(\mathbf{x}) \\ &= (1-\lambda) \cdot L_R(\mathbf{z}_{\Gamma}) + \lambda \cdot L_D(\mathbf{z}_\Gamma) \end{align}\]
  • \(A(\mathbf{x})\) : Anomaly Score이며 score 값이 클수록 anomaly이며, 작다면 이미 학습된 데이터와 유사한 이미지이다
  • \(R(\mathbf{x})\) : Residual Score \(L_R(\mathbf{z}_{\Gamma})\) 와 동일하며, 이미지의 어느 부분이 이상부분(anomalous regions)인지를 판단할수 있다
  • \(D(\mathbf{x})\) : Discriminator Score \(L_D(\mathbf{z}_\Gamma)\) 와 동일하다
  • \(\Gamma\) : 마지막번째의 update iteration을 가르킨다.

결과

비정상적인 이미지를 이용하여 비정상 탐지

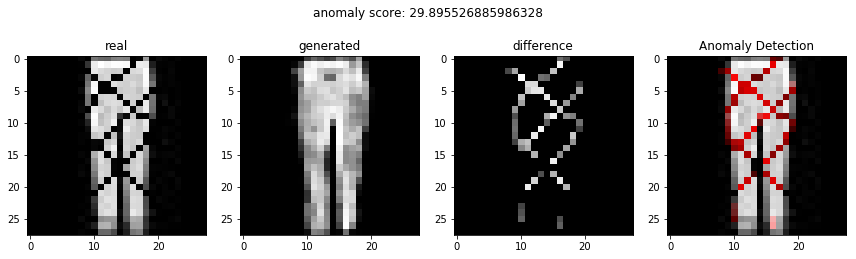
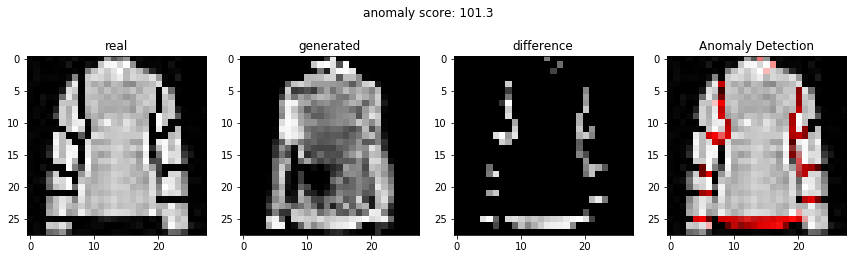
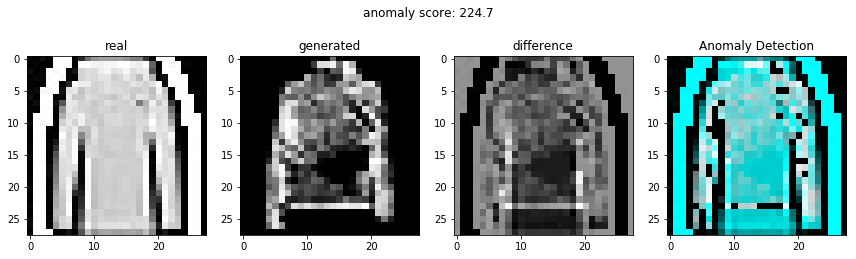
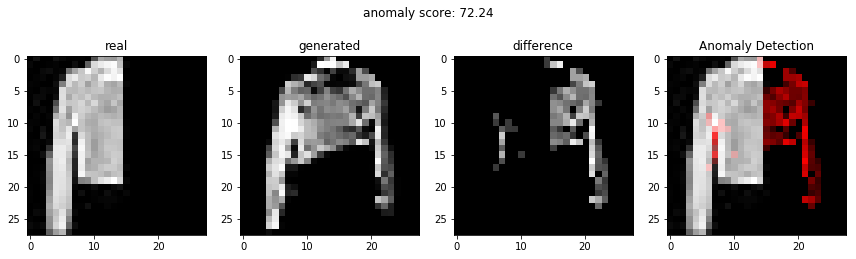
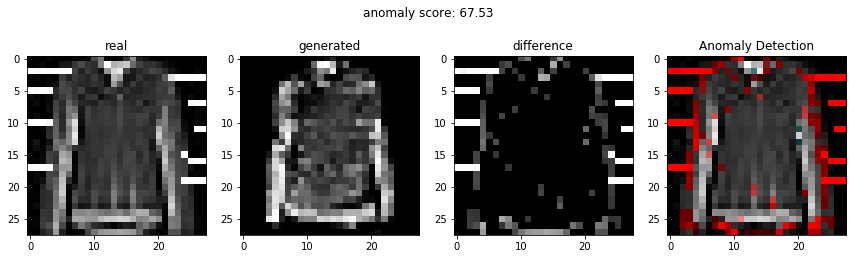
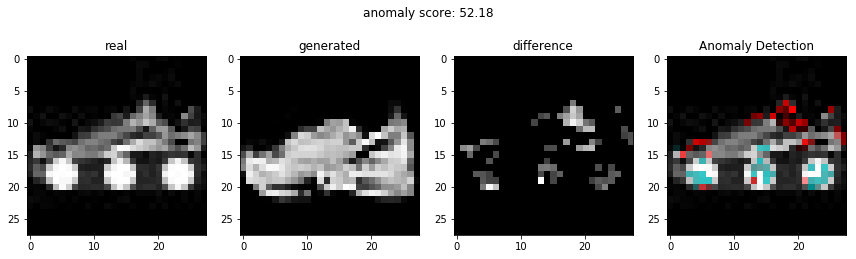
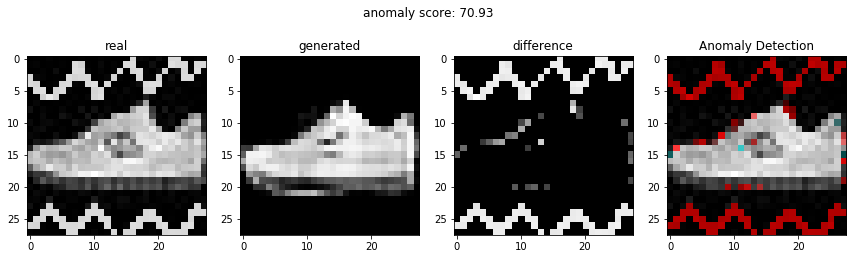
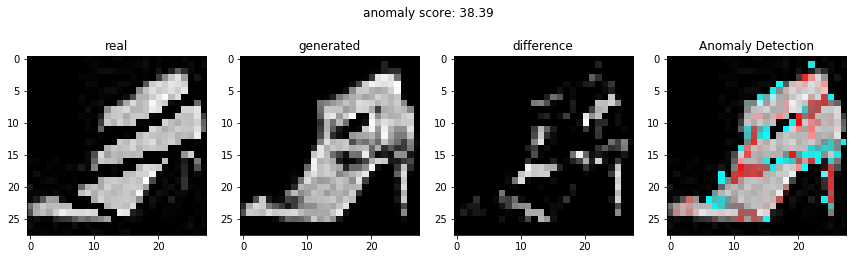
정상적인 이미지를 이용하여 비정상 탐지

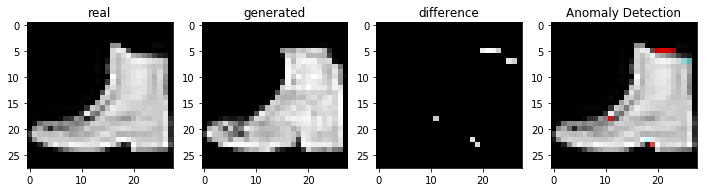
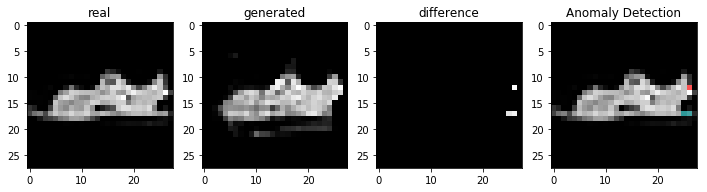
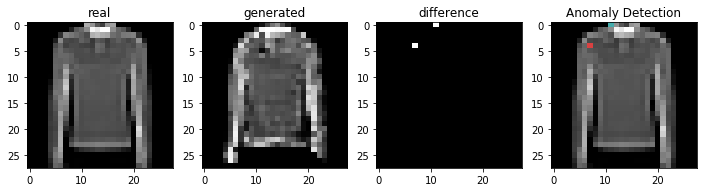
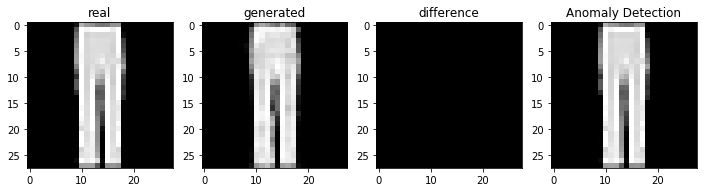
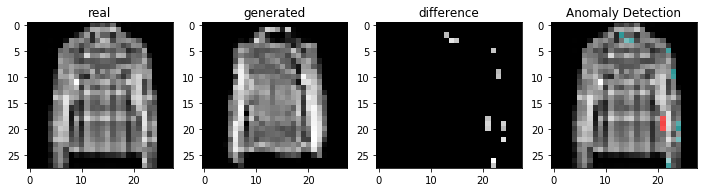
코드

아래의 주소에 있습니다.

https://github.com/AndersonJo/gan-yhat