Dense Convolution Networks
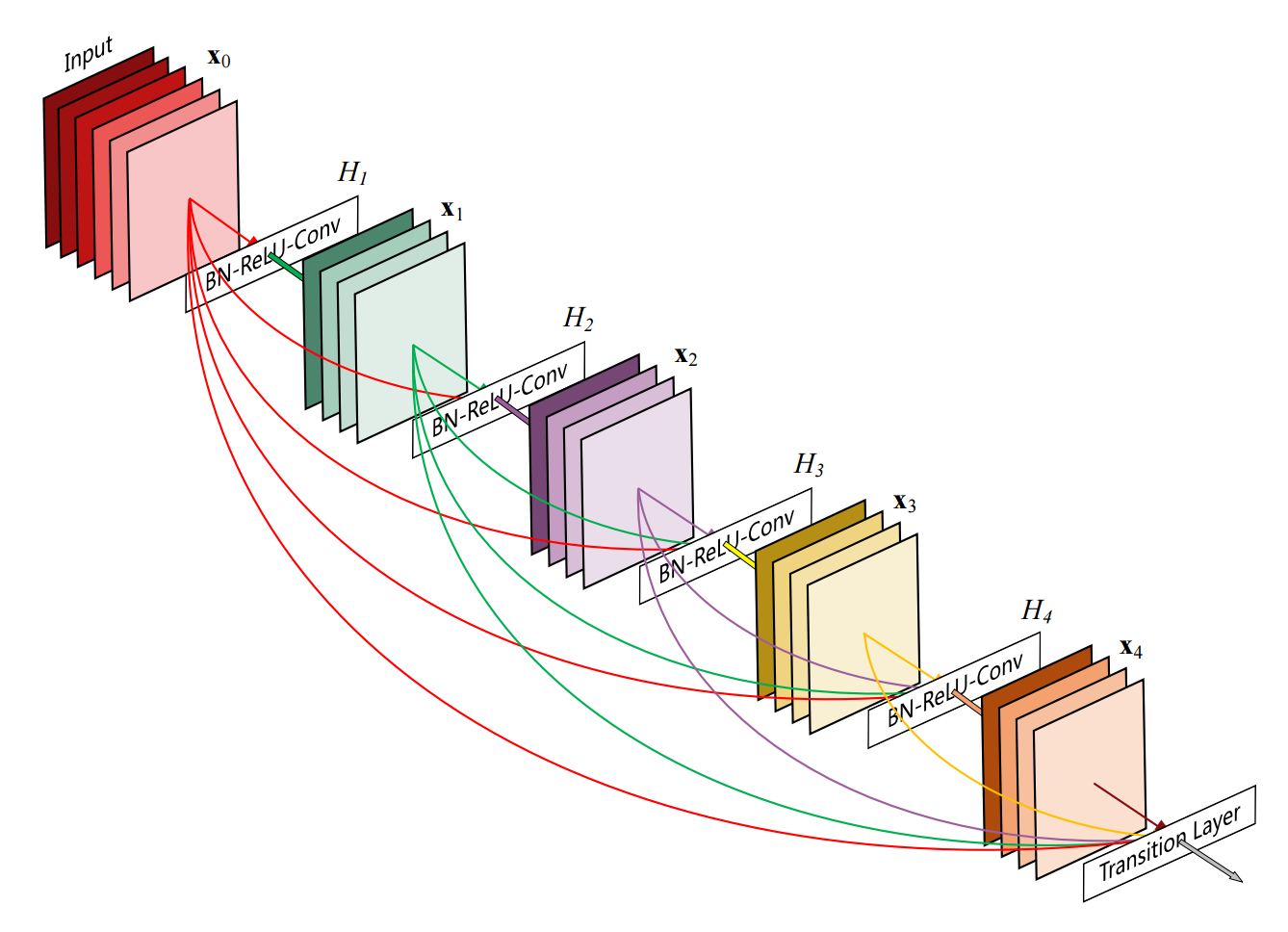
Intro
최근 연구에 따르면 convolutional networks는 input layer 또는 output layer에 가까운 layers일수록 더 정확하고, train시키기 효율적이라는 것이 증명이 되었습니다.
Dense convolutional Network (이하 DenseNet)은 이러한 이론을 받아들여 만들어졌으며, DenseNet의 모든 layer는 다른 레이어와 feed-forward 형식으로 모두 연결이 되어 있습니다.
일반적인 neural network의 경우 L layers가 있다면 L connections이 존재하나,
DenseNet에서는 \(\frac{L(L+1)}{2}\) L 개의 direct connections이 존재하며 장점은 다음과 같습니다.
- Vanishing-gradient problem을 다소 해소
- feature propagation을 강화
- 더 적은 parameters의 사용으로 메모리를 줄이고, 더 적은 computation을 요구함
Feed-Forward Networks
일반적은 convolutional feed-forward networks는 \(\mathscr{l}^{th}\) 레이어의 output을 \((\mathscr{l} +1)^{th}\)의 input으로 연결시키며 다음과 같은 형식을 갖고 있습니다.
\[\mathbf{y}_{\mathscr{l}} = H_{\mathscr{l}} \left( \mathbf{y}_{\mathscr{l} - 1} \right)\]- Network는 \(L\) 개의 layers를 갖고 있음
- 각각의 layers는 \(H_{\mathscr{l}}()\) non-linear transformation을 구현하며, \(\mathscr{l}\) 은 특정 layer의 index
- \(H_{\mathscr{l}}()\) 은 conposite function으로서 Batch Normalization (BN), rectified linear units (ReLU), Pooling, 또는 Convolution (Conv) 등등을 포함
- \(\mathscr{l}\) layer의 output을 \(\mathbf{y}_{\mathscr{l}}\) 로 표현
Residual Networks
ResNet의 경우에는 skip-connection을 추가하였으며, identity function으로 non-linear transformations을 통과시킵니다.
ResNet의 장점으로는 gradient값이 나중 레이어에서 -> 이전 레이어로 직접적으로 적용 (gradient flow)되지만,
identity function과 \(H_{\mathscr{l}}\) 의 합은 information flow를 막습니다.
ConvNet에서 ResNet은 input값을 conv, batch normalization, pooling 등을 거치고 난 값과 더합니다.
이때 pooling이 적용되었다면, 동일하게 input값에도 적용해서 shape을 맞춰줍니다.
이렇게 더해준뒤 activation을 적용하거나 아예 뺄기도 합니다.
자세한 내용은 Training Residual Nets을 참고 합니다.
Residual block architecture
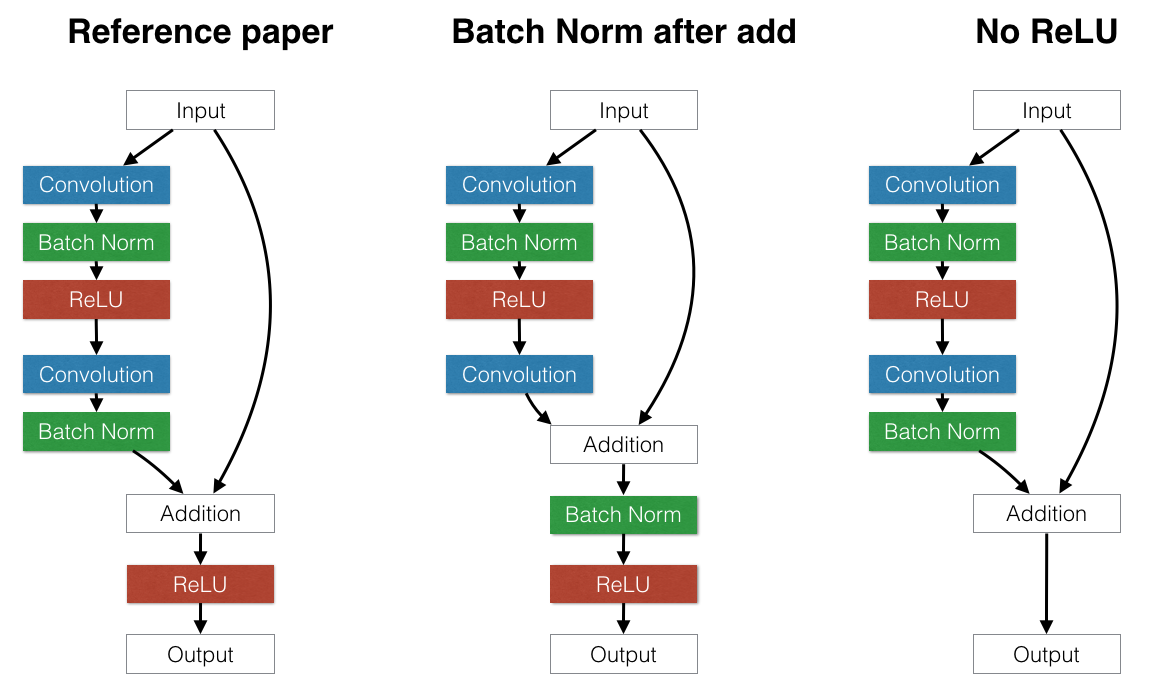
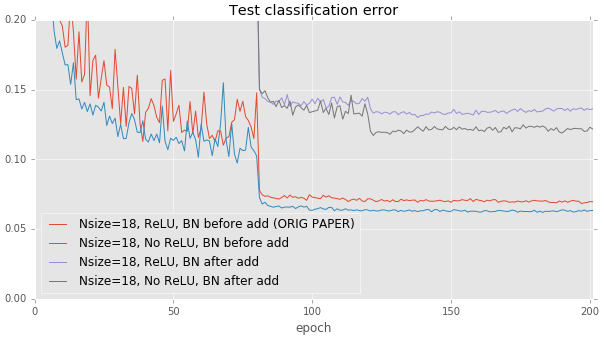
Classification Error Result
결론적으로 ReLU를 제거하고, Batch Normalization은 Addition을 하기 전에 해주는 것이 좋습니다.
Dense Convolution Networks (DenseNet)
Dense Connectivity
궁극적으로 DenseNet은 모든 레이어를 연결함으로서 information flow를 강화하였습니다.
아래의 공식처럼 \(\mathscr{l}^{th}\) 레이어는 그 이전의 모든 레이어의 feature-maps을 input으로 받습니다.
여기서 \(\left[ \mathbf{y}_0, \mathbf{y}_1 , ..., \mathbf{y}_{\mathscr{l}-1}\right]\)의 의미는 feature-maps들의 concatenation을 의미합니다.
Initial Convolution
DenseNet의 가장 첫번째 layer는 feature-maps 의 크기를 변경시키는 convolution입니다.
해당 convolution은 Channel의 크기를 변경시키며 그 외의 Input의 이미지 싸이즈등은 변경하지 않습니다.
설정은 다음과 같습니다.
| Name | Example 1 | Example 2 |
|---|---|---|
| In Channel Size | 3 | 동일 |
| Out Channel Size | 16 또는 \(2k\) 로 설정 (k는 growth rate) | 동일 |
| Kernel Size | 3 | 1 |
| Stride | 1 | 1 |
| Padding | 1 | 0 |
| Bias | False | False |
Bottleneck Layers
3 x 3 convolution앞에 bottleneck layer로서 1 x 1 convolution을 놓아서 feature-maps의 갯수를 줄일수 있습니다.
특히 1 x 1 convolution은 DenseNet에서 매우 효과적으로 움직이며 논문에서는 다음과 같은 \(H_{\mathscr{l}}\)에서 효과적이었다고 말합니다.
BN -> ReLU -> Conv(1x1) -> BN -> ReLU -> Conv(3x3)
1 x 1 Conv의 설정은 다음과 같이 합니다.
| Name | Value |
|---|---|
| In Filter Size | 각 레이어마다 growth rate \(k * (\mathscr{l} - 1) + k_0\) 를 사용 |
| Out Filter Size | \(k\) * 4 (여기서 k는 growth rate) |
| Kernel Size | 1 x 1 |
| Stride | 1 |
| Padding | 0 |
Dense Layers
Composite function \(H_{\mathscr{l}}()\) 는 다음의 순서를 갖은 operations을 의미합니다.
- Batch Normalization (BN)
- Rectified Linear Unit (ReLU)
- 3 x 3 Convolution (Conv)
| Name | Value |
|---|---|
| In Filter Size | Bottleneck의 output size ( \(k * 4\) ) |
| Out Filter Size | growth rate \(k\) |
| Kernel Size | 3 |
| Stride | 1 |
| Padding | 1 |
Transition Layer
Dense Connectivity에 있는 공식에서 concatenation operation이 사용이 됩니다.
하지만 concatenation operation은 feature-maps의 크기가 달라지면 적용을 할 수가 없게 됩니다.
DenseNet에서는 feature-maps의 크기가 달라지는 pooling layer부분을 해결하기 위해서 network를 multiple densely connected dense blocks 으로 나누었습니다.

block 사이에 있는 layers들을 transition layers 라고 하며, convolution 그리고 pooling을 가르킵니다.
논문에서는 transition layers를 다음과 같이 구성하였습니다.
- Batch Normalization Layer
- 1 x 1 Convolution Layer
- 2 x 2 Average Pooling Layer
모델의 효율화를 위해서 transition layer에서 feature-maps의 갯수를 compression factor \(\theta\) 값에 따라서 줄여줍니다.
이때 compression factor 는 \(0 \lt \theta \le 1\) 사이의 값을 갖으며,
\(\theta = 1\)일경우 dense block에서 output으로 내놓은 feature-maps의 갯수는 transition layer에서 변경되지 안습니다. DnseNet-C 모델에서는 \(\theta = 0.5\) 로 주었습니다.
Last Layer
마지막 dense layer에서는 transition을 타지 않습니다.
transition은 dense layer사이에서만 진행이 됩니다.
마지막 dense layer이후에는 global average pooling이 실행됩니다.
또는 다음과 같이 진행이 될 수 도 있습니다.
Last Dense Layer -> Batch Normalization -> ReLU -> Global Average Pooling -> Squeeze (Flatten) -> FC Layer
Growth Rate
Growth rate란 마친 0~1사이의 값을 갖은 값이라고 생각이 들텐데 전혀 아닙니다.
Growth rate를 쉽게 말하면 DenseNet의 hyper-parameter의 하나이며, 특정 dense layer의 feature-maps 의 크기를 결정짓습니다.
특정 \(\mathscr{l}\)의 feature-maps의 크기 (filter size)는 다음과 같은 공식으로 구할 수 있습니다.
- \(k_0\): Input 이미지의 채널값 입니다. 이미 초기 convolution을 거쳤기 때문에 값은 24, 48, 80 같은 값이 될 것입니다.
- \(\mathscr{l}\): 1부터 시작을 합니다.
from mpl_toolkits.mplot3d import Axes3D
def growth_rate(k, l, c=3):
return k * (l - 1) + c
K = np.arange(0, 15)
L = np.arange(0, 15)
K, L = np.meshgrid(K, L)
Z = growth_rate(K, L)
fig = plt.figure(1)
ax = Axes3D(fig)
ax.set_xlabel('K (input feature maps)')
ax.set_ylabel('L (layers)')
ax.set_zlabel('Size')
ax.plot_wireframe(K, L, Z, rstride=1, cstride=1, label='Growth Rate')
ax.grid()
ax.legend()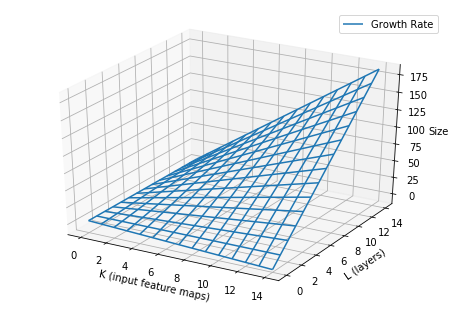
Network가 지나치게 커지는 것을 막기 위해서 k의 값은 대략 작은 값으로 제한합니다. (예.. \(k = 12\))
여기서 k의 값은 hyper-parameter로 두며 논문에서는 작은값.. (12, 24, 40) 등으로도 충분한 결과를 내놓고 있다고 합니다.
DenseNet Architecture for ImageNet
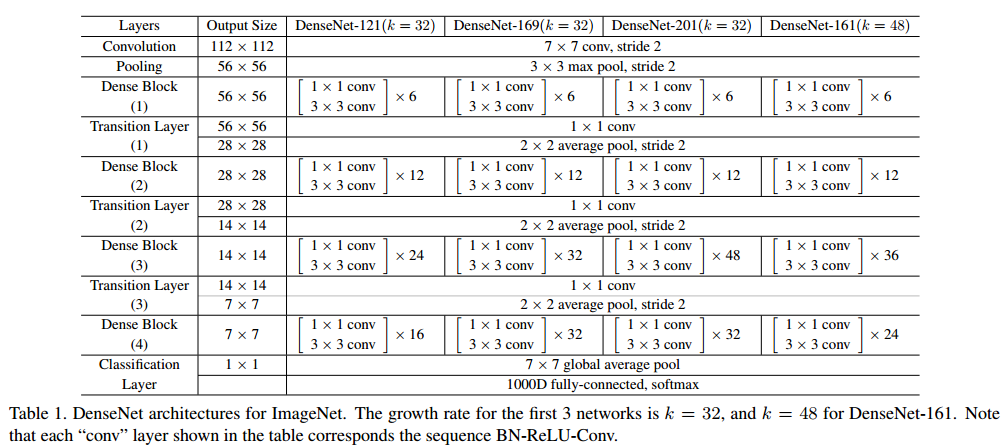
- 3개의 dense blocks을 갖고 있으며, 각각의 dense blocks은 모두 동일한 갯수의 레이어를 갖고 있음
- Input image는 먼저 convolution을 태워서 16 또는 growth rate의 2배값이 되는 output channels을 내놓음
- 모든 3 x 3 convolution의 모든 input images는 1 pixel zero-padding을 함으로서 feature-map의 크기가 변경되지 않도록 함
- Dense blocks사이에는 transition layer를 사용
- Transition layers들은 1 x 1 convolution을 통해 feature-maps size를 줄이고, 2 x 2 average pooling을 적용함
- 마지막 dense block에서는 global average pooling 그리고 softmax classifier을 적용
- 3개의 dense blocks의 feature-maps sizes는 각각 32 x 32, 16 x 16, 그리고 8 x 8
논문에서 DenseNet 구조는 다음과 같이 실험이 되었습니다.
| Name | Layer \(L\) | growth rate \(k\) |
|---|---|---|
| DenseNet | 40 | 12 |
| DenseNet | 100 | 24 |
| DenseNet with bottleneck | 100 | 12 |
| DenseNet with bottleneck | 250 | 24 |
| DenseNet with bottleneck | 190 | 40 |