Generative Adversarial Network
- How do GANs work
- Training Process
- Cost Function for Discriminator
- Cost Function for Generator
- Algorithm
- Global Optimality of (P_g = P_{\text{data}})
- Code - {:.} Configuration - {:.} Data(MNIST) - {:.} Discriminator - {:.} Generator - {:.} Training - {:.} Loss Visualization - {:.} Evaluate - {:.} Evaluate Discriminator

How do GANs work
GAN의 아이디어는 기본적으로 2개의 모델이 서로 경쟁하듯 학습을 하는 원리입니다.
그중 하나는 Generator로서 training data와 동일한 분포형태(distribution)을 갖는 샘플을 생성합니다.
다른 하나는 Discriminator로서 샘플 데이터가 real 인지 또는 fake인지 구분합니다.
즉 2개의 classes (real or fake)를 갖은 traditional supervised learning을 사용합니다.
쉽게 이야기하면 Generator는 가짜돈을 찍어내는 도둑놈이고, Discriminator는 가짜돈인지 진짜돈인지 구별해내는 경찰의 역활입니다.
게임에서 이기기 위해서 도둑놈(Generator)은 진짜 돈과 구별할수 없는 가짜 돈을 만들어야 합니다.
도둑놈과 경찰은 2개의 differentiable functions으로 표현이 됩니다.
| Name | Function | Cost | Input | Parameter |
|---|---|---|---|---|
| Distriminator | \(D\) | \(\theta^{(D)}\) 만 control하면서 minimize \(J^{(D)} \left( \theta^{(D)}, \theta^{(G)} \right)\) | \(x\) | \(\theta^{(D)}\) |
| Generator | \(G\) | \(\theta^{(G)}\) 만 control하면서 minimize \(J^{(G)} \left( \theta^{(D)}, \theta^{(G)} \right)\) | \(z\) | \(\theta^{(G)}\) |
위의 표안의 Cost부분에서 나와있듯이, 각각의 player의 cost값은 다른 player의 parameter에 의존하고 있지만,
상대방의 parameters를 건들일수 없기 때문에, 시나리오 자체가 optimization problem보다는 game으로 설명이 더 잘 됩니다.
Optimization문제의 해결책은 cost값의 (local) minimum을 찾는 것입니다.
Game에서의 해결책은 Nash equilibrium입니다. (Local diffenrential Nash equilibria)
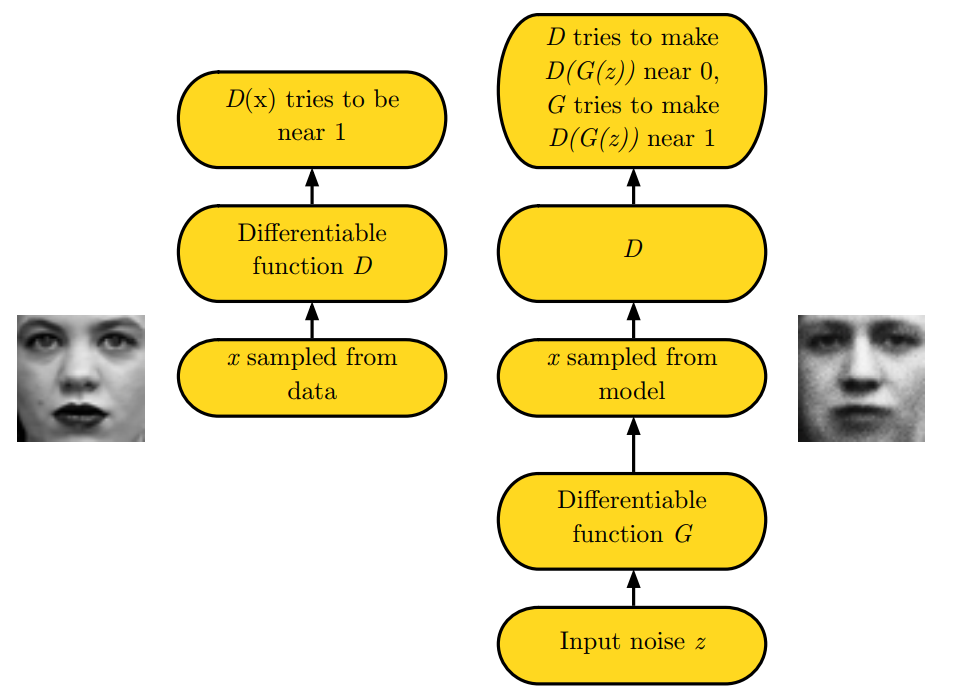
- \(D(x)\) 의 목표는 input으로 받은 데이터가 real인지에 대한 (fake가 아니라) 확률값을 output으로 내놓으며 1값으로 만드는게 목표
- \(x\) 의 절반은 data samples(real)이고, 절반은 generator가 생성산 samples(fake)입니다.
- \(D(G(z))\) -> latent variable \(z\)로부서 generator 가 x sample과 유사한 distribution을 output으로 내놓고, 해당 output은 discriminator가 input \(G(z)\)로 받습니다.
- Discriminator는 \(D(G(z))\)를 0으로 만들려고 하며, Generator는 1로 만들려고 합니다.
Training Process
Simultaneous SGD를 사용하며, 각각의 step마다 2개의 minibatches가 sampled 됩니다.
minibatch of \(x\)는 dataset으로 부터 sampled되며, minibatch of \(z\)는 latent variables로부터 만들어지게 됩니다.
이후 2개의 gradient steps이 동시에 일어나게 됩니다.
하나는 \(\theta^{(D)}\)를 업데이트하면서 \(J^{(D)}\)를 줄입니다.
다른 하나는 \(\theta^{(G)}\)를 업데이트하면서 \(J^{(G)}\)의 loss를 줄입니다.
Cost Function for Discriminator
궁극적으로 Adversarial Network는 게임 이론에서 2명의 플레이어가 참여하는 Minimax (또는 Nash Equilibrium)에서 사용하는
Value Function \(V(G, D)\)으로 표현될수 있습니다.
- \(x \sim p_{\text{data}}(x)\) 는 real data distribution 입니다.
- \(z\)는 unit gaussian distribution입니다.
- \(\big[ \log D(x) \big]\) 이부분에서 D(x)는 1로 maximize 해야 합니다.
- \(\big[ \log (1-D(G(z)) \big]\) 이부분에서 \(D(G(z))\)는 0으로 minimize해야 합니다.
실제 구현시 Discriminator의 loss function은 결론적으로 binary cross entropy loss function을 사용합니다.
아래는 일반적인 binary cross entropy의 공식입니다.
여기에서 minimax를 적용하기 위해서는 다음과 같이 공식을 수정합니다.
\[J^{(D)} \left(\theta^{(D)}, \theta^{(G)} \right) = - \frac{1}{N} \sum^N_{i=1} \Big[ \log D(x^{(i)}) + \log (1-D(G(z^{(i)})) \Big]\]\[J^{(D)} \left(\theta^{(D)}, \theta^{(G)} \right) = H(1, D(x^{(i)}) + H(0, D(G(z^{(i)})))\]실제 구현시에는 2번의 cross entropy의 사용으로 위의 공식을 구할 수 있습니다.
즉 \(\log D(x^{(i)})\) 이 부분은 \(y\) 값을 1로 주면 되고
\(\log (1-D(G(z^{(i)}))\) 이 부분은 \(y\) 값을 0으로 주면 됩니다.
Cost Function for Generator
Minimax
discriminator에 대한 cost를 함수를 정의했지만, generator에 대한 cost함수는 정의하지 않았습니다.
위에서 언급했듯이 GAN은 optimization 문제라기 보다는 서로 상대방이 싸우면서 성장하는 Game에 더 가깝다고 언급을 했습니다.
단순한 게임의 입장에서 본다면 Zero-Sum Game (모든 플레이어들의 costs의 합은 0이 됨)
즉 D, G functions은 두명이 참여하는 minimax 게임을 하고 있는 것입니다.
\[J^{(G)} = \theta^{(G)*} = \min_{G} \max_{D} V(D,G) = \mathbb{E}_{x \sim P_{data}} \left[ \log D(x) \right] + \mathbb{E}_{z \sim P_{z}(z)} \left[ \log( 1 - D(G(z)) \right]\]Heuristic, non-saturating game
Minimax를 실제 적용하면 이론처럼 잘 돌아가지 않습니다.
Discriminator는 cross entropy를 minimize시키고, Generator는 동시에 maximize시키려고 합니다.
처음에는 Discriminator가 실수를 많이 하기 때문에 loss값이 크게 나오며 이는 gradient도 커지게 되며 학습이 빠르게 일어납니다.
문제는 학습하면서 discriminator가 거의 완벽하게 잡아낼때쯤에는 loss값이 0으로 saturate되며, generator의 gradient값은 vanish가 되버립니다.
예를 들어서 Discriminator가 \(D(G(z))\) 를 높은 수치로(ex 0.0001) 분별하면 다음과 같은 일이 일어나게 됩니다.
\[\begin{align} J^{(G)} &= - \log(1-0.0001) \\ &= 0.0001000050003 \end{align}\]즉 gradient값이 너무 작아서 학습이 잘 되지를 않습니다.
논문에 따르면 오랜시간 돌리면 결국 학습이 된다고는 합니다. 하지만 제가 했을때 100번의 epochs에도 학습이 안되었습니다.
위의 문제를 해결하기 위해서 crossentropy 를 계속 사용하되, sign 값을 뒤바꿔주는것이 아니라, crossentropy 에서 사용되는 target부분을 뒤바꿔줍니다.
\[J^{(G)} = \mathbb{E}_{z \sim P_{z}(z)} \Big[\log D(G(z))\Big]\]해당 버젼의 게임에서는 원래 Minimax에서는 누군가 이기고, 누군가 지게 되는 상황인데,
누군가 지게(losing)되는 상황에서 강한 gradient를 갖도록 만듭니다.
Heuristic, non-saturating game에서는 더이상 zero-sum게임이 아니게 됩니다.
Algorithm
논문에 나온 Algorithm 입니다.
Minimax사용하여 구현하였으며, 실제 구현시 G의 update부분은 heuristic으로 변경하는게 좋습니다.

Global Optimality of \(P_g = P_{\text{data}}\)
G는 고정되어있다고 가정하고, optimal discriminator D는 다음과 같습니다.
\[D^*_{G}(x) = \frac{ P_{\text{data}}(x) }{ P_{\text{data}}(x) + P_g(x)}\]Code
전체코드는 Anderson Jo - GAN 에서 확인하실수 있습니다.
Configuration
BATCH_SIZE = 32Data(MNIST)
train = MNIST('./data', train=True, download=True, transform=transforms.Compose([
transforms.ToTensor(), # ToTensor does min-max normalization.
]), )
test = MNIST('./data', train=False, download=True, transform=transforms.Compose([
transforms.ToTensor(), # ToTensor does min-max normalization.
]), )
# Create DataLoader
dataloader_args = dict(shuffle=True, batch_size=BATCH_SIZE ,num_workers=1, pin_memory=True)
train_loader = dataloader.DataLoader(train, **dataloader_args)
test_loader = dataloader.DataLoader(test, **dataloader_args)Discriminator
class Discriminator(nn.Module):
def __init__(self):
super(Discriminator, self).__init__()
self.fc1 = nn.Linear(784, 441)
self.fc2 = nn.Linear(441, 256)
self.fc3 = nn.Linear(256, 32)
self.fc4 = nn.Linear(32, 1)
self.bc1 = nn.BatchNorm1d(441)
self.bc2 = nn.BatchNorm1d(256)
def forward(self, x):
x = x.view((-1, 784))
h = self.fc1(x)
# h = self.bc1(h)
h = F.leaky_relu(h)
h = F.dropout(h, p=0.2, training=self.training)
h = self.fc2(h)
# h = self.bc2(h)
h = F.leaky_relu(h)
h = F.dropout(h, p=0.2, training=self.training)
h = self.fc3(h)
h = F.leaky_relu(h)
h = self.fc4(h)
out = F.sigmoid(h)
return out
D = Discriminator()
print(D.cuda()) # CUDA!
d_optimizer = optim.Adam(D.parameters(), lr=0.001)Generator
class Generator(nn.Module):
def __init__(self):
super(Generator, self).__init__()
self.fc1 = nn.Linear(100, 196)
self.fc2 = nn.Linear(196, 289)
self.fc3 = nn.Linear(289, 361)
self.fc4 = nn.Linear(361, 400)
self.fc5 = nn.Linear(400, 512)
self.fc6 = nn.Linear(512, 625)
self.fc7 = nn.Linear(625, 784)
self.fc8 = nn.Linear(784, 784)
self.bc1 = nn.BatchNorm1d(196)
self.bc2 = nn.BatchNorm1d(289)
self.bc3 = nn.BatchNorm1d(361)
self.bc4 = nn.BatchNorm1d(400)
self.bc5 = nn.BatchNorm1d(512)
self.bc6 = nn.BatchNorm1d(625)
self.bc7 = nn.BatchNorm1d(784)
def forward(self, x):
h = self.fc1(x)
h = self.bc1(h)
h = F.leaky_relu(h)
h = F.dropout(h, p=0.5, training=self.training)
h = self.fc2(h)
h = self.bc2(h)
h = F.leaky_relu(h)
h = F.dropout(h, p=0.5, training=self.training)
h = self.fc3(h)
h = self.bc3(h)
h = F.leaky_relu(h)
h = F.dropout(h, p=0.5, training=self.training)
h = self.fc4(h)
h = self.bc4(h)
h = F.leaky_relu(h)
h = F.dropout(h, p=0.4, training=self.training)
h = self.fc5(h)
h = self.bc5(h)
h = F.leaky_relu(h)
h = F.dropout(h, p=0.4, training=self.training)
h = self.fc6(h)
h = self.bc6(h)
h = F.leaky_relu(h)
h = F.dropout(h, p=0.4, training=self.training)
h = self.fc7(h)
h = self.bc7(h)
h = F.leaky_relu(h)
h = F.dropout(h, p=0.4, training=self.training)
h = self.fc8(h)
out = F.sigmoid(h)
return out
G = Generator()
print(G.cuda())
g_optimizer = optim.Adam(G.parameters(), lr=0.001)Training
# Train Discriminator with Generator not being trained
# 먼저 Discriminator를 학습시킵니다.
# 이때 real image와 fake이미지 두개의 데이터를 사용하여 학습합니다.
# Discriminator를 학습시킬때는 Generator는 학습시키면 안됩니다.
N_EPOCH = 100
real_y = Variable(torch.ones((BATCH_SIZE, 1)).cuda())
fake_y = Variable(torch.zeros((BATCH_SIZE, 1)).cuda())
loss_f = nn.BCELoss()
d_real_losses = list()
d_fake_losses = list()
d_losses = list()
g_losses = list()
divergences = list()
Train Discriminator with Generator not being trained
# 먼저 Discriminator를 학습시킵니다.
# 이때 real image와 fake이미지 두개의 데이터를 사용하여 학습합니다.
# Discriminator를 학습시킬때는 Generator는 학습시키면 안됩니다.
for epoch in range(N_EPOCH):
for step, (real_images, _) in enumerate(train_loader):
# Samples
real_images = Variable(real_images.cuda())
z = Variable(torch.randn((BATCH_SIZE, 100)).cuda())
###############################################
# Train D (But do not train G)
###############################################
# Init D
d_optimizer.zero_grad()
# Calculate the loss with real images
y_real_pred = D(real_images)
d_real_loss = loss_f(y_real_pred, real_y)
# Calculate the loss with fake images
fake_distributions = Variable(torch.randn((BATCH_SIZE, 100)).cuda())
fake_images = G(fake_distributions).detach()
y_fake_pred = D(fake_images)
d_fake_loss = loss_f(y_fake_pred, fake_y)
# Update D with G not being updated
d_loss = d_real_loss + d_fake_loss
d_loss.backward()
d_optimizer.step()
###############################################
# Train G with fake images but do not train G
###############################################
g_optimizer.zero_grad()
fake_distributions = Variable(torch.randn((BATCH_SIZE, 100)).cuda())
fake_images = G(fake_distributions)
y_pred = D(fake_images)
g_loss = loss_f(y_pred, real_y)
g_loss.backward()
g_optimizer.step()
###############################################
# Visualization
###############################################
if step%5 == 0:
d_real_losses.append(d_real_loss.data[0])
d_fake_losses.append(d_fake_loss.data[0])
d_losses.append(d_loss.data[0])
g_losses.append(g_loss.data.cpu().numpy()[0])
divergences.append(torch.mean(y_real_pred/(y_real_pred+y_fake_pred)).data[0])
if step % 50 == 0:
print(f'\r[{epoch+1}/{N_EPOCH}]',
# '{:.3}'.format(torch.mean(params[0]).data[0]),
'divergence: {:<8.3}'.format(np.mean(divergences[-100:])),
'D: {:<8.3}'.format(np.mean(d_fake_losses[-100:])),
'D_real: {:<8.3}'.format(np.mean(d_real_losses[-100:])),
'D_fake: {:<8.3}'.format(np.mean(d_fake_losses[-100:])),
'G:{:<8.3}'.format(np.mean(g_losses[-100:])), end='')
print()Loss Visualization
def smooth(x,window_len=100,window='hanning'):
x = np.array(x)
if x.ndim != 1:
raise ValueError("smooth only accepts 1 dimension arrays.")
if x.size < window_len:
raise ValueError("Input vector needs to be bigger than window size.")
if window_len<3:
return x
if not window in ['flat', 'hanning', 'hamming', 'bartlett', 'blackman']:
raise ValueError("Window is on of 'flat', 'hanning', 'hamming', 'bartlett', 'blackman'")
s=numpy.r_[x[window_len-1:0:-1],x,x[-1:-window_len:-1]]
if window == 'flat': #moving average
w=numpy.ones(window_len,'d')
else:
w=eval('numpy.'+window+'(window_len)')
y=numpy.convolve(w/w.sum(),s,mode='valid')
return y
figsize(16, 6)
plot(smooth(d_real_losses), label='D(x) Loss')
plot(smooth(d_fake_losses), label='D(G(z)) Loss')
plot(smooth(g_losses), label='G(z) loss')
plot(smooth(divergences), label='divergences')
grid()
legend()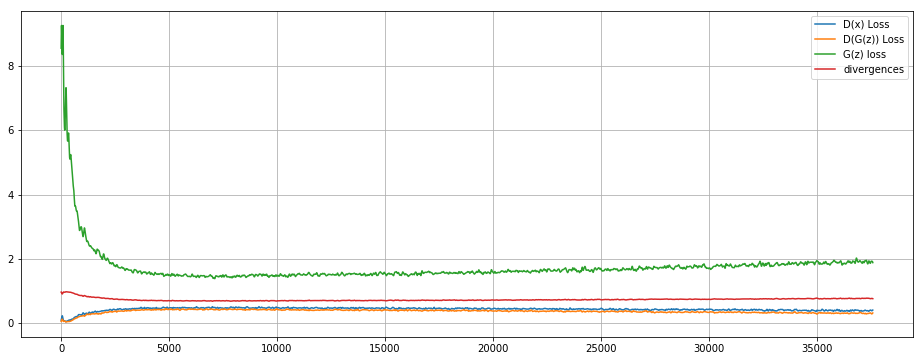
Evaluate
fake_distributions = Variable(torch.randn((BATCH_SIZE, 100)).cuda())
images = G(fake_distributions).view((-1, 28, 28)).data.cpu().numpy()
imshow(images[0], cmap=cm.gray_r)
fig, subplots = pylab.subplots(4, 7) # subplots(y축, x축 갯수)
idx = 0
for _subs in subplots:
for subplot in _subs:
d = images[idx]
subplot.get_xaxis().set_visible(False)
subplot.get_yaxis().set_visible(False)
subplot.imshow(d, cmap=cm.gray_r)
idx += 1

Evaluate Discriminator
n_test = test_loader.dataset.test_data.size()[0]
y_test_real_labels = np.ones((n_test, 1))
y_test_fake_labels = np.zeros((n_test, 1))
# Predict Real Images
test_data = Variable(test_loader.dataset.test_data.cuda().type_as(torch.cuda.FloatTensor()))
y_test_real_pred = D(test_data)
# Predict Fake Images
fake_distributions = Variable(torch.randn((n_test, 100)).cuda())
fake_images = G(fake_distributions).detach()
y_test_fake_pred = D(fake_images)
# Evaluate
y_test_real_pred = torch.round(y_test_real_pred).data.cpu().numpy()
y_test_fake_pred = torch.round(y_test_fake_pred).data.cpu().numpy()
print('Discriminator Real Image Accuracy:', accuracy_score(y_test_real_labels, y_test_real_pred))
print('Discriminator Fake Image Accuracy:', accuracy_score(y_test_fake_labels, y_test_fake_pred))Discriminator Real Image Accuracy: 0.8037
Discriminator Fake Image Accuracy: 0.9195