검도학원 다닐때 목검으로 내리치는 것만 수천번 하더군요. 그것도 한 자세로만요.
마찬가지로 cost functions도 머리속에서 공식이 바로 그려지고 특성까지 파악될 정도로 연습을 해야 한다고 생각합니다.

Gradient Descent Optimization Algorithms

일단 Optimizer 시리즈를 시작하기전에 optimizer를 안썼을때와 비교하기 위해서 SGD를 먼저 공개합니다.
본문에서 다룰 내용은 vanilla gradient descent 라고 불리는 batch gradient descent를 다루고,
그 다음에 stochastic gradient descent를 다룹니다.

데이터가 작고, 실험정도라면 batch gradient descent가 더 높은 accuracy를 보여주지만,
실제 실무에서는 쓰이지 않으며, 많은 양의 데이터를 다뤄야하는 인공지능의 특성상 전혀 안쓰인다고 보면 됩니다.
Stochastic gradient descent도 실제 실무에서는 쓰이지 않습니다.
두개의 알고리즘 모두 이론적이며 학문적인것이긴 하나 또 몰라서도 안됩니다.
아주 기초적인 내용이기 때문입니다.

다음과 같이 표기

  • Weights (parameters): \(\theta\) 이며.. 이때 \(\theta \in R^d\) 이다.
  • Objective Function: \(J(w)\)
  • Gradient of the objective function: \(\nabla_\theta J(\theta)\)

Import Libraries

%pylab inline
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error

Data

data = np.loadtxt('../../data/linear-regression/ex1data1.txt', delimiter=',')
X = data[:, 0].reshape(data[:, 0].shape[0], 1) # Population
Y = data[:, 1].reshape(data[:, 1].shape[0], 1) # profit

# Standardization
scaler_x = StandardScaler()
scaler_y = StandardScaler()
X = scaler_x.fit_transform(X)
Y = scaler_y.fit_transform(Y)

scatter(X, Y)
title('Profits distribution')
xlabel('Population of City in 10,000s')
ylabel('Profit in $10,000s')
grid()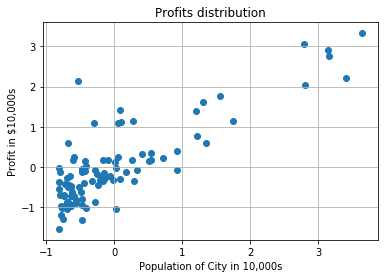

Batch Gradient Descent (Vanilla Gradient Descent)

Gradient Descent를 할때 전체 training dataset을 사용해서 구합니다.
\(\nabla\) 는 derivativation을 가르키고, \(\Delta\) 는 차이점을 가르킴

\[\theta = \theta - \eta \cdot \nabla_\theta J( \theta)\]

즉 weights(parameters) 한번을 업데이트 하기 위해서 전체 dataset을 다 돌려야 하기 때문에 매우 느리며, 메모리에 다 들어가지도 않는 경우가 많습니다. 또한 실시간으로 새로운 데이터가 입력되는 (on-the-fly)상황에서도 전체 데이터를 다 돌려야 하기때문에 적용을 할 수 없습니다.

아래는 참고로.. derivative of \(J(\theta)\) 했을때..

\[\frac{\partial}{\partial \theta} = \Delta \theta = \frac{2}{N} \sum^N_{i=1} -x_i(y_i - \sum_{j=0}(\theta_j x_j ))\] \[\frac{\partial}{\partial b} = \Delta b = \frac{2}{N} \sum^N_{i=1} -(y_i - \sum_{j=0}(\theta_j x_j))\] 
w = np.array([-0.1941133,  -2.07505268]) # np.random.randn(2)

def predict(w, X):
    N = len(X)
    yhat = w[1:].dot(X.T) + w[0]
    yhat = yhat.reshape(X.shape)
    return yhat

def batch_gradient_descent(X, Y, w, eta=0.1):
    N = len(X)
    yhat = predict(w, X)
    delta =  Y - yhat
    w_delta = 2/N * np.sum(-delta.T.dot(X))
    b_delta = 2/N * np.sum(-delta)

    w[1:] = w[1:] - eta * w_delta
    w[0] = w[0] - eta * b_delta
    return w

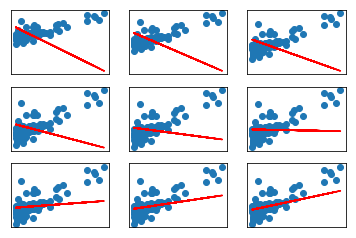
for i in range(1, 10):

    w = batch_gradient_descent(X, Y, w)

    yhat = predict(w, X)

    axes = subplot(3, 3, i)
    axes.get_xaxis().set_visible(False)
    axes.get_yaxis().set_visible(False)

    scatter(X, Y)
    plot(X, yhat, color='red')
    grid()
    axes.grid()

    yhats = np.where(yhat >= 0.5, 1, 0)
    accuracy = mean_squared_error(Y, yhats)
    print('Mean Squared Error (less is good):', accuracy)

Mean Squared Error (less is good): 1.9776853516
Mean Squared Error (less is good): 1.7253375238
Mean Squared Error (less is good): 1.0
Mean Squared Error (less is good): 1.0
Mean Squared Error (less is good): 1.0
Mean Squared Error (less is good): 1.0
Mean Squared Error (less is good): 0.725250038743
Mean Squared Error (less is good): 0.686136644177
Mean Squared Error (less is good): 0.637070721578

Stochastic Gradient Descent

SGD의 경우는 완전 반대로 weights(parameters) 업데이트를 각각의 traning data \(x^{(i)}\) 그리고 label \(y^{(i)}\)마다 합니다.

\[\theta = \theta - \eta \cdot \nabla_\theta J( \theta; x^{(i)}; y^{(i)})\] 
w = np.array([-0.1941133,  -2.07505268])

def sgd(X, Y, w, eta=0.1):
    N = len(X)
    for i in range(N):
        x = X[i]
        y = Y[i]
        yhat = predict(w, x)
        delta = y - yhat

        w_delta = 2/N * np.sum(-delta.T.dot(x))
        b_delta = 2/N * np.sum(-delta)

        w[1:] = w[1:] - eta * w_delta
        w[0] = w[0] - eta * b_delta
    return w



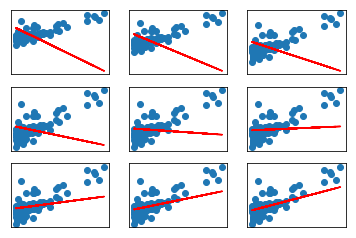
for i in range(1, 10):
    w = sgd(X, Y, w)
    yhat = predict(w, X)

    axes = subplot(3, 3, i)
    axes.get_xaxis().set_visible(False)
    axes.get_yaxis().set_visible(False)

    scatter(X, Y)
    plot(X, yhat, color='red')
    grid()
    axes.grid()

    yhats = np.where(yhat >= 0.5, 1, 0)
    accuracy = mean_squared_error(Y, yhats)
    print('Mean Squared Error (less is good):', accuracy)

Mean Squared Error (less is good): 1.9851376897
Mean Squared Error (less is good): 1.76244027984
Mean Squared Error (less is good): 1.0423548062
Mean Squared Error (less is good): 1.0
Mean Squared Error (less is good): 1.0
Mean Squared Error (less is good): 1.0
Mean Squared Error (less is good): 1.0
Mean Squared Error (less is good): 0.725250038743
Mean Squared Error (less is good): 0.686136644177

References